I have a brand new piece of IP. How shall I verify it?
 |
The digital design industry appears to me to be bifurcated. There are design engineers and then there are verification engineers. Designs are built, and then thrown over a wall (a.k.a. “delivered”) to the verification team to be “verified”. The verification team then finds a bug and throws (sends) the design back to the design team to be fixed and so forth.
The verification team tends to use one of several methodologies then to verify
the design. Many of these methodologies involve using the System Verilog
Assertion language
to describe how the design is supposed to work, and then
trying to find what it takes to break the design. Often, this approach
makes extensive use of automatically generated cover() statements to
make certain every piece of logic within a design has been reached.
 |
To understand the issues associated with this divide, let’s look at it from the verification team’s perspective. Imagine someone just handed you a large and complex design, and then asked you to verify it. This isn’t just an academic exercise, since I’ve had the opportunity to examine such RISC-V designs as the Pulp-Platform’s Ri5cy CPU, or Western Digital’s SWERV processor. Most recently, I had the opportunity to apply my formal AXI properties to the Pulp-Platform’s AXI-Lite crossbar.
In each of these examples, I had the opportunity to play (some of) the role of the Verification Engineer. I was given a large and complex design that I had never seen before, and then was asked to find a bug within it.
Where would you start?
Read the fine manual.
Sure, but what would your next step be?
In my case, I started by treating each processor as a black box, to which I attached any interface property sets I had to it. I then ran a bounded model check until I ran out of patience. In the case of the Western Digital’s SWERV processor, I added an AXI property set to their I/Os and only made it about 20 time steps into the design. In the case of the Pulp-Platform’s AXI-Lite crossbar, I added my AXI-lite property sets and then only made it about 14 steps into the design. With Ri5cy, I attached the riscv-formal property set to the CPU. Once done, I was able to discover that the Ri5cy CPU had six bugs in the first 12 time steps. After those 12 time steps, the process came to an absolute brick wall, and I couldn’t go any further.
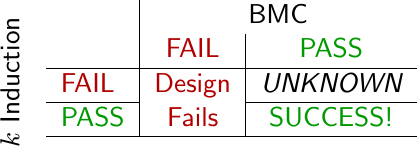 |
Might there be a bug on timestep 40? Absolutely! When you only use a bounded proof, it’s hard to know if the first 20 timesteps are sufficient for verifying a core or not.
This is very different from the way I go about verifying my own designs. When I verify one of my own designs, I use induction to verify the design for all time. This is often called an “unbounded” proof. I will examine the design for some number of time steps from the beginning of time, and then again using induction for some number of timesteps at some arbitrary point later in time. The resulting proof is then valid for all time–not just the first 10-20 time steps.
The amount of formal-processing work isn’t really all that different. For example, in the ZipCPU, I can verify the entire CPU using an unbounded proof. The proof only requires between 8 and 18 steps, depending upon how the CPU is configured.
Why can’t I do this with one of these other CPU’s?
I suppose I could–theoretically. The problem is that I would then need to get to know how these CPU’s work in a deeper depth than the designers ever knew and understood when they built their various cores in the first place. Let’s take a moment to dig into this, and see why this is so. We’ll look at an AXI-lite proof, an AXI slave, and then some example CPU proofs along the way.
The AXI-Lite Crossbar
At the core of the issue is the question of whether or not formal verification is a form of white or black box testing. To answer this question, let’s consider a generic set of bus properties for discussion, and then examine how those would get applied to a crossbar.
- Everything gets cleared following a reset
- Whenever the bus is stalled, the request doesn’t change
- There should be no acknowledgments without a prior request
- All requests should (eventually) get a response
Two of these properties are particularly problematic. These are the third and fourth ones. They are problematic simply because they require state within the property checker–state that can get out of alignment with the rest of the design under test if you aren’t careful.
Let’s look at how we might implement the property that there should be no
acknowledgments without a prior request. The first thing we’d need is a
counter to keep track of all of the outstanding transactions–transactions
that still need returns. Let’s call this counter f_outstanding.
always @(posedge i_clk)
if (i_reset)
f_outstanding <= 0;
else case({ bus_request, bus_response })
2'b10: f_outstanding <= f_outstanding + 1;
2'b01: f_outstanding <= f_outstanding - 1;
endcaseNow that we know how many requests are outstanding, we can assert that there shouldn’t be any bus acknowledgments without a prior request.
always @(posedge i_clk)
if (bus_response)
assert(f_outstanding > 0);Now, let me ask you, what would it take to verify this property? With a bounded proof, it’s not that hard: you just follow the design from time-step one through the end of your patience, and you know the design will be internally consistent.
But was that enough time steps? You might never know.
How about that unbounded proof then? This would be the proof that verifies your assertions for all time. For this you need induction.
Yes, there are some solvers that can handle unbounded proofs with no more work. Such solvers include ABC’s IC3 solver, called “abc pdr” in SymbiYosys, or the Avy or Super-Prove Aiger solvers. The problem with these solvers is that they work great on simple problems, but tend to struggle on the more complex problems. Even worse than that, when they struggle it’s hard to tell why.
To go after the large and complex proofs, you will need an SMT
solver such as
Yices or
Boolector. (BTOR looks like a promising
upgrade over SMT, but I have only limited experience with it to date.) These
solvers need a little
guidance in order to handle an unbounded proof. This guidance comes in the
form of assertions, contained within the design, that the design will be
consistent. In this case, we’ll need to make certain that the design is
consistent with the f_outstanding counter from our property checker.
For example, when verifying Xilinx’s AXI-lite cores, I was able to add,
always @(*)
assert(faxil_awr_outstanding == faxil_wr_outstanding);This works because Xilinx’s core never accepted any write address transactions into the core without also accepting the write data transaction at the same time.
Similarly, once a write request is accepted, Xilinx’s demo core immediately acknowledged it. That allowed me to write,
always @(*)
assert(faxil_wr_outstanding == (o_axi_bvalid ? 1:0));I can now write similar properties for the read side of the core, and the various outstanding transaction counters are now fully matched to the state within the core.
My own AXI-lite slave demonstration design doesn’t work like that at all. In order to achieve 100% throughput, the design uses an internal skid buffer. When using a skid buffer, there may be an outstanding transaction within the buffer that needs to be counted. In that case, the assertion looks more like,
always @(*)
assert(faxil_wr_outstanding == (o_axi_bvalid ? 1:0)
+ (!o_axi_wready ? 1:0));since the core will drop WREADY any time something is in the
skid buffer.
A similar assertion can then be used to constrain the number of outstanding
write address requests.
These assertions are easy to write. Indeed they are fairly trivial–to me the designer.
What happens, though, when you get to a crossbar interconnect? In that case, the assertions get more challenging to write.
Let’s take a look, for example, at the assertion that relates the outstanding
counter in the master’s properties to those of the slaves properties.
This needs to be done for every one of the various masters
who might have made
AXI-lite
requests of the core. In this design, there are NM of them, corresponding
to each of the NM masters connecting to the crossbar that might each wish
to talk to one of the NS slaves.
generate for(N=0; N<NM; N=N+1)
begin : CORRELATE_OUTSTANDINGFor each master, we have to ask the question of whether or not they’ve been
granted access to a particular slave. This information is captured by
swgrant[N] which, within my
design,
indicates that master N has been granted access to a slave, and also by
swindex[N], which gets populated with the index of the slave that master N
has been granted access to. If swindex[N] == NS, then the master has
been granted access to a non-existent slave whose sole purpose is to return bus
errors.
always @(*)
if (S_AXI_ARESETN && (swgrant[N] && (swindex[N] < NS)))
beginNow, for every master who’s been granted access to a slave, we can then
correlate the number of outstanding transactions from the masters perspective,
fm_awr_outstanding[N], with the number of outstanding transactions from the
slaves perspective, fs_awr_outstanding[swindex[N]]. This correlation needs
to take into account the
skid buffer
on the input, the extra clock stage (optionally) used to
determine which slave a request needs to be assigned to, as well as any
responses that have yet to be accepted.
assert((fm_awr_outstanding[N]
- (S_AXI_AWREADY[N] ? 0:1)
-((OPT_BUFFER_DECODER && dcd_awvalid[N]) ? 1:0)
- (S_AXI_BVALID[N] ? 1:0))It needs to equal the slave’s counter of outstanding write address transactions,
fs_awr_outstanding[swindex[N]], adjusted for any requests waiting to be
accepted in the slave, or being returned from the slave and waiting
to be accepted by the master.
== (fs_awr_outstanding[swindex[N]]
+ (m_axi_awvalid[swindex[N]] ? 1:0)
+ (m_axi_bready[swindex[N]] ? 0:1)));The process then needs to be repeated for the write data channel–although it’s still roughly the same equation as the write address channel we just looked at.
assert((fm_wr_outstanding[N]
- (S_AXI_WREADY[N] ? 0:1)
- (S_AXI_BVALID[N] ? 1:0))
== (fs_wr_outstanding[swindex[N]]
+ (m_axi_wvalid[swindex[N]] ? 1:0)
+ (m_axi_bready[swindex[N]] ? 0:1)));But what about all of the other channels that haven’t (yet) been granted access to any slaves, or for whom the grant is to our non-existent, bus error producing slave? In that case, we now need to repeat the assertion–but this time it won’t depend upon the slave’s counter of outstanding transactions at all–just the master’s counter.
end else if (S_AXI_ARESETN && (!swgrant[N] || (swindex[N]==NS)))
begin
if (!swgrant[N])
assert(fm_awr_outstanding[N] ==
(S_AXI_AWREADY[N] ? 0:1)
+((OPT_BUFFER_DECODER && dcd_awvalid[N]) ? 1:0)
+(S_AXI_BVALID[N] ? 1:0));
else
assert(fm_awr_outstanding[N] >=
(S_AXI_AWREADY[N] ? 0:1)
+((OPT_BUFFER_DECODER && dcd_awvalid[N]) ? 1:0)
+(S_AXI_BVALID[N] ? 1:0));
assert(fm_wr_outstanding[N] ==
(S_AXI_WREADY[N] ? 0:1)
+(S_AXI_BVALID[N] ? 1:0));
end
//
// We'll skip the similar assertions for the read channel(s)
// ...
//
end endgenerateNow, let me ask you, how complex is this assertion to write and express?
All we’ve done is create an assertion to correlate the state within the design with the number of outstanding transactions the crossbar expects. That allows us to make the assertion that there shall be no responses without a prior request–the same thing we started with. As with the two example AXI-lite slaves, we’re still correlating the state of the internal crossbar with that of the various counters found within the AXI-Lite property checkers. However, unlike the very simple AXI-lite slaves, this assertion is now much more complex than the original one we started out with.
What would happen if we didn’t have these complex and design-dependent assertions? In the case of the crossbar, the solver would find 4 time-steps ending such that the master had no outstanding transactions, but where there was also a bus response being returned from one of the slaves. The solver would then conclude the design was in error.
Why only 4 time-steps? Simply because that’s how I have the proof set up–since I am able to verify the AXI-lite crossbar in only four time steps, I do so.
Would it help to add more time steps? Not really. The solver would always be able to find more time-steps with outstanding transactions, only to return a contradiction on the last step. Proving this to students is one of the exercises in the formal verification course that I teach.
Your turn: Verify an AXI slave
So, now, let me ask you: if this was not your design, would you ever add such a complex assertion to the design? If you were a “verification engineer”, who had been handed this design for the purpose of verifying it, would you add this assertion? Would you even know where to look to find all the registers that needed to be included to do so?
If you didn’t add the assertion to the design, you wouldn’t be able to accomplish an unbounded proof. You’d be stuck verifying the design for a bounded proof only and never knowing if you’d missed anything.
So, who should add these properties then? Are properties like these the responsibility of the design team or the verification team?
For those who have never used formal verification, this complexity is cited as a reason not to use it.
For the verification engineer looking over a design with no internal properties, he’d be tempted to just look at a bounded check of the design. If the bounded check finds something, the verification engineer can claim he’s earned his pay for that day.
But what if it doesn’t find anything? In frustration, he might decide to just run simulations looking for property violations. Perhaps he might use a lot of cover checks to convince himself that the simulations were sufficient, much like Xilinx did when verifying their AXI ethernet-lite design, and so miss the fact (as Xilinx did) that writes to the core might be applied to the wrong address if they arrived on the same clock cycle as a read request.
To the designer, on the other hand, this property isn’t nearly as complex. Why not? Because it’s his design. The designer knows every stage in his design, where transactions might get stalled, where they might hide, and where to check when getting this count right. As the designer of the AXI-lite crossbar, above, I know there’s a skid buffer on entry. I know the parameter that enables or disables it. I know that the address decoder might, or might not, require a clock–and which parameter option controls that.
These are things an engineer might not be aware of who examines the design from a black box perspective alone.
But lets be serious, what’s the likelihood of hitting a bug in a crossbar more than 14 steps into the design? In this case, it’s actually higher than you might expect. Every crossbar needs counters within it to know how many transactions are outstanding, so that it can tell when a channel may be reassigned to another master-slave pair. It is the responsibility of the crossbar to make certain these counters don’t overflow. You aren’t likely to overflow one of these counters inside 14 timesteps.
CPU Verification
The same basic concepts apply when verifying a CPU, although they will look different. A CPU contains instructions that get passed through various stages of processing as they direct reads from the register file, writes to the register file, and reads from or writes to memory. To verify a CPU, therefore, you want to follow an instruction through the CPU and make sure that it does the “right thing” at every stage.
The riscv-formal project does this based upon a packet of information that is produced by a piece of logic scaffolding added to the CPU. Within the riscv-formal parlance, this is called the “RISC-V Formal Interface” or RVFI. Once the packet is fully formed, the attached property set can make assertions about what the CPU did.
For example, if the instruction was an ADD instruction, then it should’ve read from the two given registers, summed their values together, and then written the result back to the destination register before retiring. riscv-formal captures these separate pieces together in its insn_add logic.
assign spec_valid = rvfi_valid && !insn_padding && insn_funct7 == 7'b 0000000 && insn_funct3 == 3'b 000 && insn_opcode == 7'b 0110011; wire [4:0] insn_rs2 = rvfi_insn[24:20];
wire [4:0] insn_rs1 = rvfi_insn[19:15];
// ...
assign spec_rs1_addr = insn_rs1;
assign spec_rs2_addr = insn_rs2;-
What were their values?
In the riscv-formal setup, the values of the instructions are provided by the CPU core, and only checked by a separate register value checker.
wire [RISCV_FORMAL_XLEN-1:0] result = rvfi_rs1_rdata + rvfi_rs2_rdata;
// ...
assign spec_rd_wdata = spec_rd_addr ? result : 0;Once these portions of the instruction have been decoded, the check for this instruction can then be written simply as,
always @*
if (!reset && spec_valid && !spec_trap)
begin
// If the source register is used, it must match
if (spec_rs1_addr != 0)
assert(spec_rs1_addr == rs1_addr);
if (spec_rs2_addr != 0)
assert(spec_rs2_addr == rs2_addr);
// The destination register must match
assert(spec_rd_addr == rd_addr);
// The instruction result must match the result of an
// addition, as expected
assert(spec_rd_wdata == rd_wdata);
// The next instruction must have an address 4 bytes later
// (for an add instruction)
assert(`rvformal_addr_eq(spec_pc_wdata, pc_wdata));
//
// Other properties, not relevant to an ADD
//
endThis is, of course, a paraphrase. The actual instruction check also needs to check for potential memory operations (not used in an add instruction), and so on.
Further, the riscv-formal
approach to verifying a RISC-V processor has a unique
twist to it–it treats instructions as separate individual checks, and allows
the processor to do whatever it wants for N-1 clock cycles, only to insist
that the Nth clock cycle contains an addition (if checking additions), and
so on. I understand these choices to be made for performance reasons
appropriate for bounded checks only.
Let’s see how this plays out when examining a couple of CPU’s: Ri5cy and the ZipCPU–which doesn’t use riscv-formal, but rather uses an unbounded approach.
The Ri5cy Processor
Some years ago, I was asked to apply the riscv-formal properties to the Ri5cy processor. Ri5cy is a RISC-V processor built as part of the PULP Platform. The PULP Platform was built as part of a joint project between ETH Zurich and the Univerty of Bologna. You can also read more about the PULP Platform here.
My task was simple: all I needed to do was to find the various signals within the core that corresponded to the various components of the riscv-formal interface. Once these various signals were made available to the external environment, the riscv-formal properties could then be applied to find the bugs in the CPU.
Did I find bugs? Yes. My report described six bugs that I found using the Symbiotic EDA Suite. Were these bugs major? Not this time. Most of the major bugs had been worked out by the time I got to the core. As a result, most of what I found revolved around properly decoding HINT instructions.
Or so I thought.
Some time later, Ashish Dhabari of Axiomise had the opportunities to look at Ri5cy’s two sibling processors: Zero-Ri5cy and Micro-Ri5cy. He found several issues with these two processors, to include several with the core’s debugging interface as well as a situation that would cause the CPU to deadlock.
Why didn’t I find these bugs? The obvious answer is that I wasn’t tasked with verifying the debugging interface, and so I disabled it early on when it created problems. Moreover, I only looked through the first 12 timesteps, and that’s not a long period of time to find deadlock issues.
I also know that I really struggled to identify the various signals within the Ri5cy core that could be used to properly populate the RVFI packet. Indeed, it felt like I needed to reverse engineer the CPU to do so. One of the surprises that I had to deal with was the fact that Ri5cy might retire a memory instruction on the same cycle as it retires a subsequent ALU operation. This took me a long time to figure out. Indeed, I found myself using the formal tools to debug my own properties long before I was debugging any instruction properties.
I think I might have found more bugs, however, if I was able to convert my proof into an unbounded proof using induction. That said, long after I had “verified” the ZipCPU, I still found a deadlock bug within it, so there’s still something to be said for looking for such bugs particularly.
The ZipCPU Processor
So what would it take to convert the riscv-formal approach to one that would work for an unbounded check? Simple–the RVFI packet would need to be followed through all the processing steps of the CPU. At each stage, the RVFI packet would need to be checked against the CPU’s internal state. Such properties would not be required in any bounded check, but in my own experience they are required for any unbounded proofs.
This is basically how the ZipCPU’s verification flow works. It’s the same basic principle: create a packet of information describing the instruction being processed, and then follow that packet of information as it works its way through the CPU.
The two big differences? First, the ZipCPU is not a RISC-V CPU, and second the ZipCPU’s proof is an unbounded proof. To make the unbounded proof work, the ZipCPU’s formal instruction packet is double checked against the CPU for consistency purposes at every stage of the pipeline.
Let’s look at the read-operands stage of the ZipCPU’s pipeline as an arbitrary example. This stage is defined first and foremost by the instruction within it. When the pipeline steps forward, the instruction from the decode stage steps forward into the read-operands stage.
always @(posedge i_clk)
if (op_ce)
begin
f_op_insn_word <= f_dcd_insn_word;
f_op_phase <= dcd_phase;
// ...
endA special, formal verification-only, instruction decoder is then used to decode the various components of this instruction.
f_idecode #(.ADDRESS_WIDTH(AW),
.OPT_MPY((IMPLEMENT_MPY!=0)? 1'b1:1'b0),
.OPT_EARLY_BRANCHING(EARLY_BRANCHING),
.OPT_DIVIDE(IMPLEMENT_DIVIDE),
.OPT_FPU(IMPLEMENT_FPU),
.OPT_LOCK(OPT_LOCK),
.OPT_OPIPE(OPT_PIPELINED_BUS_ACCESS),
.OPT_SIM(1'b0),
.OPT_CIS(OPT_CIS))
f_insn_decode_op(f_op_insn_word, f_op_phase, op_gie,
fc_op_illegal, fc_op_Rid, fc_op_Aid, fc_op_Bid,
fc_op_I, fc_op_cond, fc_op_wF, fc_op_op, fc_op_ALU,
fc_op_M, fc_op_DV, fc_op_FP, fc_op_break, fc_op_lock,
fc_op_wR, fc_op_rA, fc_op_rB, fc_op_prepipe,
fc_op_sim, fc_op_sim_immv
);This decoder is special because all of its results are combinatorial. That’s important: there’s no state within it to check. Instead, the combinatorial outputs are checked against the ZipCPU’s state.
The results of this “formal-only” decoder can then be compared with the internal values found within the CPU’s pipeline. Here, for example, is a small portion of that check:
always @(posedge i_clk)
if ((op_valid)&&((f_op_branch)||(!fc_op_illegal))&&(!clear_pipeline))
begin
if (!op_illegal && !f_op_branch)
begin
// If it's an ALU instruction, make sure it's
// flagged as such
assert(fc_op_ALU == op_valid_alu);
// ... same for a memory instruction
assert(fc_op_M == op_valid_mem);
// ... and a divide instruction
assert(fc_op_DV == op_valid_div);
// ... and a (yet to be implemented) floating point
// instruction
assert(fc_op_FP == op_valid_fpu);
// Make sure the register ID of operand A matches
assert(fc_op_rA == op_rA);
// Make sure the register ID of operand B matches
assert(fc_op_rB == op_rB);
// Make sure whether or not this instruction writes
// to the flags register matches whether or not its
// supposed to
assert(fc_op_wF == op_wF);
// Make sure the resulting ID register matches
assert(fc_op_Rid[4:0] == op_R);
// Make certain that the "is-this-a-lock instruction"
// flag matches
assert(fc_op_lock == op_lock);
// Make certain that the "is-this-a-break instruction"
// flag matches
assert(fc_op_break == op_break);
// ...
//
// ...
// ...This forces consistency between the instruction word,
f_op_insn_word, that’s working it’s way through the
pipeline,
and the various signals within
the CPU
which should have been determined properly from the instruction word.
Your turn: Verify a CPU
Now, imagine you were handed a large CPU and told that it needed to be verified. How would you go about it?
Would you create a large simulation script, designed to exercise every CPU instruction, to then verify that the CPU worked? This was my initial approach to verifying the ZipCPU. You can read about all the bugs this script missed here. You can read about the problems I had with my instruction cache here. Indeed, in just my first experience with formal methods, I learned that such a scripted simulation approach was prone to failure.
The industry understanding of formal verification is that a specialized verification engineer should examine a given core, one that he didn’t write, and then write formal properties for it.
Pardon me for saying it, but … this doesn’t make any sense!
You want a verification engineer, someone who isn’t familiar with the core he is supposed to verify, who doesn’t understand the internals of how the core operates, to verify that the core has no bugs in it? Do you want him to reverse engineer the core to get there?
Wouldn’t it make more sense for the designer to build his own formal properties?
Sure, a verification engineer could do this work. However, he would be swimming upstream to do this. Would it work? That might depend upon your verification engineer–since he’d need to be more capable than the design engineer to do this. The original core designer, on the other hand, would get much farther with the same tools for the simple reason that the designer already knows his own design.
Conclusions
My point is simply this: The greatest benefit from using formal methods comes during design, not during some later verification stage run by a separate engineering team.
During design, one simple formal statement can drive a lot of testing. During design, formal properties will give you more bang for your engineering time than a simulation script will. It will check more of your designs functionality, and find more bugs. You can read about what that might look like here.
The ideal place for simulation isn’t really before running the formal tools, it’s after running those same tools.
Even better, if the designer has already run the formal tools on his design, he can then pass the design to a verification engineer with the formal properties still attached. This will give the verification engineer a leg up when attempting to verify that the core truly will live up to its design or not.
The lord of that servant shall come in a day when he looketh not for him, and in an hour that he is not aware of, (Matt 24:50)
