An Exercise in using Formal Induction
In many ways I’m still quite the beginner when it comes to proving designs using formal methods: I’ve only used formal methods for about about five months. However, over those five months I’ve found so many bugs in my “working” code that I’ve started using formal methods for every new component and design I’ve built since.
I’ve also found myself counseling others on the #yosys IRC forum. It’s been rather strange, though, since I very much feel as though I myself am quite the beginner, and yet I’m answering questions and explaining things as though I’d been doing this for years.
I haven’t.
However, I’d like to share with you today an example piece of code that really taught me a lot about formal methods, and in particular about the induction step. It’s come up recently as I’ve tried to explain induction to someone with even less experience than I have, and I’ve found that it makes a good and simple example to learn from.
I’ll be honest–my own mentors haven’t thought that much of the example below. Their response has been something like, “Oh, yes, of course.” Yet to me, I’ve found this example to be very instructive.
The Example Code
The basic example
consists of two shift registers, sa and sb, although
the example would also work if you were comparing Fibonacci versus Galois
linear feedback shift registers
(LFSR)s–it just wouldn’t be
nearly as clear. However, the example does require that the two
shift register outputs need to be identical.
 |
We’ll allow our two shift registers to have a parameterized
length, LN, although for the purposes of today’s discussion we’ll only
set this length to a constant 16, LN=16.
module kitest(i_clk, i_reset, i_ce, i_in, o_bit);
parameter LN=16;
//
input wire i_clk, i_reset, i_ce, i_in;
output wire o_bit;
reg [(LN-1):0] sa, sb;For this example to be instructive, both shift registers must have identical logic. Therefore, we’ll initialize both registers to zero.
initial sa = 0;
initial sb = 0;We’ll clear both registers on any synchronous reset.
always @(posedge i_clk)
if (i_reset)
begin
sa <= 0;
sb <= 0;
endFinally, any time i_ce is true, the input value will be placed into the
least significant bit (LSB) of each shift register, while we shift the rest
of the register to the left.
else if (i_ce)
begin
sa <= { sa[(LN-2):0], i_in };
sb <= { sb[(LN-2):0], i_in };
endIn all other clocks, sa and sb will remain unchained.
Our example needs an output, so let’s set our output value to be the exclusive OR of the most significant bits in each register.
assign o_bit = sa[LN-1] ^ sb[LN-1];If these two shift registers are truly identical, then we should be able to assert this fact to the formal solver, as in:
`ifdef FORMAL
assert property(!o_bit);If you stop here and try to prove this one property,
`endif
endmoduleit will pass a bounded model check, but not induction.
Once I understood why this simple design struggled with induction, I was suddenly able to figure out why various designs were struggling with induction, and I then understood how to deal with it. Therefore, let’s spend the rest of this article discussing the difficulty with this design, and also how we might go about solving it.
Running SymbiYosys
If you have SymbiYosys installed, then all it takes is a very simple script to run this test. Since adjusting parameters is fairly easy with SymbiYosys, we’ll use it for our tests today.
There are four basic parts to any SymbiYosys script: the options, the formal engine, the yosys script, and the list of component files involved.
In our case, we’ll want to use the formal mode prove. This will run both the bounded model checker (BMC), and the induction engine. Other modes I’ve worked with include bmc, which just runs the bounded model checker, and cover, which checks cover properties. SymbiYosys also supports a mode for checking liveness, called mode live, but I have yet to try that mode.
[options]
mode prove |
We’ll also be adjusting the depth of the proof. This is the number of logic
steps the formal solver uses to test our design. In bmc mode, this will
be the number of clock cycles, measured from the beginning of time, that
are checked for any assertion failures. For the
induction step, in
prove mode, this will decide the number of clock cycles for both the bmc
pass and the
induction pass. For
the induction pass,
all but the last cycle will assume your assert’s are true. On the last cycle,
however, the formal engine will try to find one example where it can show that
an assertion fails.
In my initial SymbiYosys script, I’ll set this depth to 31.
depth 31As I mentioned, we’ll be adjusting this value during today’s exercise.
We’ll also need to specify which formal solving engine we want to use. In this case, the yices engine will work quite nicely.
[engines]
smtbmc yicesOther engines are available, and may produce different results.
We’ll then provide SymbiYosys with a very simple set of yosys commands to build our test,
[script]
read_verilog -formal kitest.v
prep -top kitest
[files]
kitest.vBe aware when you are working with
SymbiYosys
that the [files] section
will specify where your source files are coming from.
SymbiYosys will then copy
these files to a working directory before running
yosys,
so the read_verilog command within the
yosys
[script] section will reference all files
from within the current directory where
SymbiYosys placed them.
Let’s save this script to a file, kitest.sby. Put together, the whole SymbiYosys script will look like,
[options]
mode prove
depth 31
[engines]
smtbmc yices
[script]
read_verilog -formal kitest.v
prep -top kitest
[files]
kitest.vAssuming you have SymbiYosys, yosys, and yices installed, then all it then takes to run SymbiYosys is the command,
% sby -f kitest.sbyPay attention to the last line returned by SymbiYosys. If all goes well, you’ll get the line:
SBY [kitest] DONE (PASS, rc=0)However, if our design passes BMC (which it will) but fails induction, then this last line will instead read,
SBY [kitest] DONE (UNKNOWN, rc=4)In the next section, we’ll look at what happens when we apply SymbiYosys to our example.
Exploring what happens
Let’s spend some time exploring what happens within this example design, and see what it will take to get us to fully prove our property that the output bit will always be zero.
We’ll start out by describing a set of tests, each containing a different
approach to handling this problem. We’ll use the local parameter
FORMAL_TEST to select from among several possible options for proving
this.
localparam [2:0] FORMAL_TEST = 3'b001;
generate if (FORMAL_TEST == 3'b000)
begin
always @(*)
assume(i_ce);
end else if (FORMAL_TEST == 3'b001)
begin
// No extra logic
end else if (FORMAL_TEST == 3'b010)
begin
assert property(sa == sb);
end else if (FORMAL_TEST == 3'b011)
begin
always @(posedge i_clk)
if (!$past(i_ce))
assume(i_ce);
end else if (FORMAL_TEST == 3'b100)
begin
always @(posedge i_clk)
if ((!$past(i_ce))&&(!$past(i_ce,2)))
assume(i_ce);
// else
// No formal logic
end endgenerateNow, let’s work our way through these tests, shall we?
When FORMAL_TEST is zero, the test passes–much as we might expect.
Since it does pass, there’s no trace generated to examine and we can move
on. We’ll come back to this, though, in a moment.
When FORMAL_TEST is set to 3'b001, however, the test fails. Why would
this be? It doesn’t make sense, right? I mean, if you look at the
code,
you can clearly (by examination) tell that sa==sb, and so there must be
something wrong with the
formal methods,
therefore, if it can’t tell that these two are equal.
Well, not quite. Let’s dig a little deeper.
In particular, let’s pull up the trace associated with this failure. If you look through the SymbiYosys output, you’ll find the line ending with
.... Writing trace to VCD file: engine_0/trace_induct.vcdWe can open trace_induct.vcd in GTKWave
and look at what’s going on here. You’ll find this file in the
kitest/engine_0 directory where
SymbiYosys
placed it.
 |
If you look through the trace, you’ll notice that sa and sb are
indeed different.
What? How can this be?
To understand this, you need to understand a bit about how formal induction works. The induction step works by picking random initial values for every registered signal within the design. Well, okay, that’s not quite right. The values aren’t truly chosen randomly, they are actually chosen exhaustively. Were they chosen randomly, it might be possible to miss some choices that would cause the design to fail. The benefit of formal, however, is that it will try every possible combination in order to find one that will cause your design to fail. To you as a developer looking at the traces through your code, it might feel like these values are chosen randomly, although there’s actually a method to this madness.
Either way, the engine knows nothing about whether or not the design could ever achieve the initial values it chooses. It only knows whether or not any of these violate any assumptions or assertions.
For the first 31 steps of this test, the only constraint upon sa and sb is
that their most significant bits are equal. The engine has kept this true for
us. Nothing in our example
constrains the rest of the shift register, either sa[LN-2:0] or sb[LN-2:0],
so those values can be anything.
Then, in step 31, the engine chooses to set i_ce high. This forces a
comparison between sa[LN-1] and sb[LN-1] on step 32, where the comparison
(which is formed by our assertion) fails.
This is obviously not what we want, so
what can we do to fix this? The most obvious answer is to
assert that sa==sb. This is FORMAL_TEST 3'b010. This test passes
very quickly, with little fanfare. This works.
What else might we do?
Suppose we went back and examined our first test again, with our depth set to 15 instead of 31. You’ll need to adjust the depth option within the SymbiYosys configuration script to do this.
depth 15As before, we can pull up the trace to see what happened.
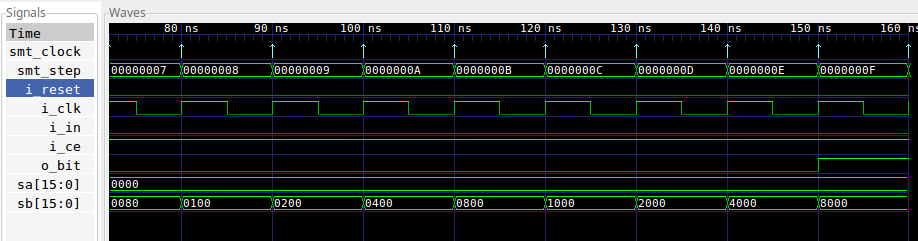 |
In this trace, sa and sb are different again. This time,
though, the difference starts out in bit zero on the first timestep (not shown).
On every clock following, this one differing bit moves one step closer to our
assertion that the most significant bits of sa andsb are identical. As
this assertion is applied in the first 15 steps, it is applied as an
assumption–forcing the fifteen most significant bits of sa and sb to be
identical. However, on step 16, the assertion
is treated not as an assumption but rather as a full-blown assertion.
This time it fails, because we never told the formal engine that bits zero
in both shift registers were initially identical.
This suggests that this test will pass for a depth of 16. Feel free to try that one on your own.
Now let’s move on and try FORMAL_TEST 3'b011.
In this test, i_ce is never allowed to be zero for two clocks in a row.
It is allowed to be true on every clock, or to alternate between true and
false, or some combination between the two.
Let’s make one more change as well. We’ll set the induction depth to 30 steps in kitest.sby.
depth 30This test also fails.
As before, we can pull up the trace to see what happened.
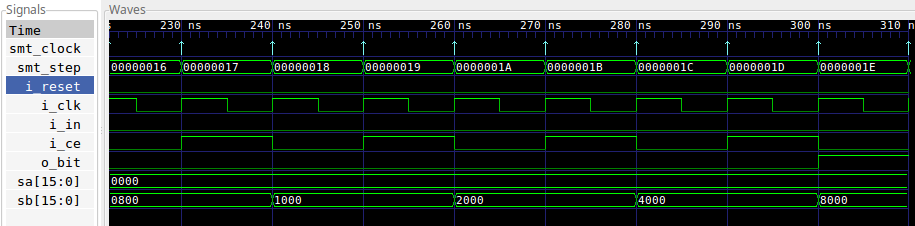 |
This looks very much like the last test that failed: both failed because the
induction engine
allowed sa and sb to start out with different least significant bit.
The only thing that’s different here is i_ce. In this case, the
induction
engine has chosen to alternate i_ce with high and low.
Why? Because the alternating i_ce value pushes the assertion regarding
this bit far enough forward in formal steps that the proof now fails.
However, it failed on the last step. I know, induction always only ever fails on its last step. That’s not what I mean. What I mean is that if we just extend the search depth by one clock,
depth 31then this test will pass.
The last test, FORMAL_TEST 3'b100, is very similar to test 3b011. I’ll
leave this one as homework for you.
I’ll also leave as homework for you the task of insisting that i_ce is
true at least one of every eight clocks cycles. How many induction steps will
that take to succeed?
I like this example, because it does a good job fleshing out how the formal induction proof works.
Reality turns out to be very similar to this example, although it never looks
as simple. In most of the designs I’ve worked with, there’s always been some
amount of state that I can’t quite capture with a proper assert statement.
By using a longer
induction
length, though, I can often force the state within my designs to flush itself.
Even this doesn’t always work.
You may remember my discussion of the formal
properties
of a wishbone
bus. Nothing within the
specification
forces a slave to drop its STALL output to accept a new request within a
given number of cycles. Likewise, nothing within the specification forces
a slave to respond to the request by raising the ACK signal within a
given number of clock cycles. This creates a possibility where there may
be some amount of hidden state. In order to deal with that possibility,
just like we forced i_ce to be high at least one in N clock cycles, I
would force
the stall line, STALL, to be dropped if it was ever asserted for too long.
In a similar fashion, I would
prevent
the slave from waiting too many clock cycles before acknowledging a request.
Other Approaches
If you have a chance to try some other formal engines, you may find they work better in this example. For example, the pdr engine,
[engines]
abc pdravy,
[engines]
aiger avyand suprove
[engines]
aiger suprovedon’t seem to struggle with this problem.
Conclusion
Induction may be the more difficult step of using formal methods. It need not be, but you need to understand how it works in order to understand the reasons while it might fail. The example above is, in my estimation, simple enough to show the difficulties with induction. If you understand the details of this example, this example, you should be ready to fully formally prove your own designs.
And thine house and thy kingdom shall be established for ever before thee: thy throne shall be established for ever. (2Sam 7:16)
