Just how long does a formal proof take to finish?

Formal methods are exhaustive in their nature. That’s what makes them special. That’s why I like using them over constrained random simulation based testing. If there’s ever a way a property within your design can be made to fail, formal methods can find it.

That’s the good news.

The bad news is that because formal methods are exhaustive they can take exponential time to complete. The bigger and more complex your design is, the longer the solver will take to prove a property. Eventually, there comes a complexity where the property becomes essentially impossible to prove.

In other words, the answer to “how long does the formal solver take to return an answer?” can be anywhere from trivial to infinite depending upon the problem.

That’s not helpful. Perhaps some statistics might be more useful.

Looking at some statistics

I’ve now been doing formal verification for almost two years, ever since my first humbling experience. Over the course of that time, I’ve kept the output directories created by SymbiYosys for nearly 900 of the proofs that I’ve completed. This includes both halves of any induction proofs, as well as quite a few cover proofs. With a bit of work, these proof durations can be organized into an approximate cumulated distribution function, such as Fig. 1 shows.

Fig 1. Proof duration CDF

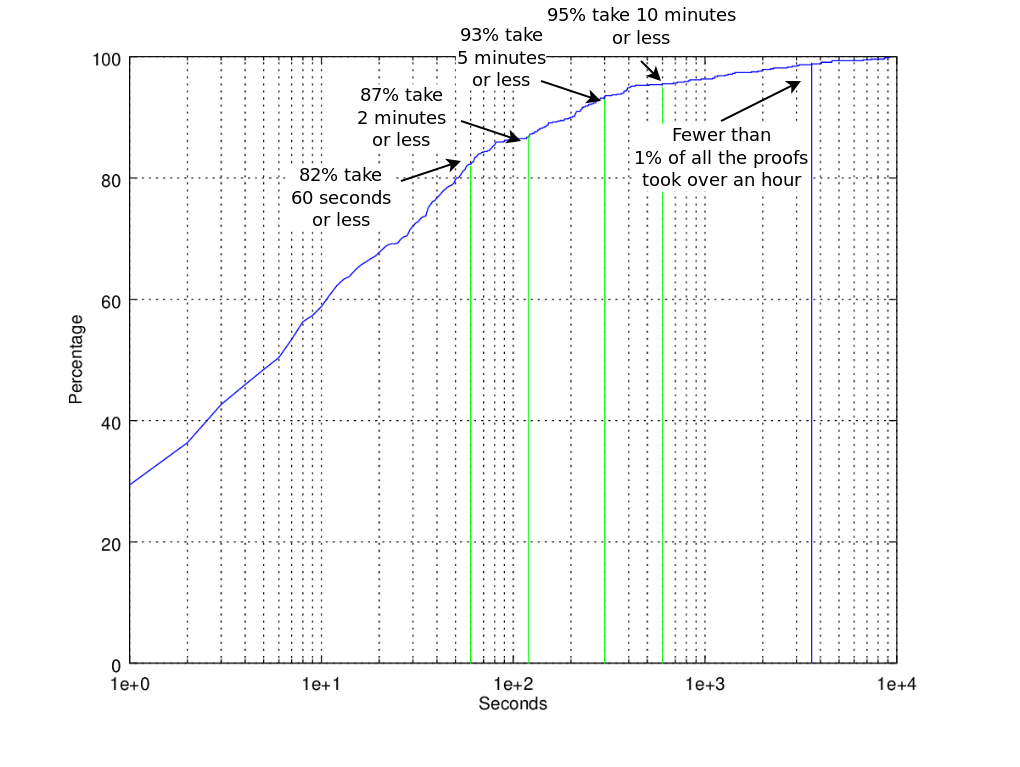In this chart, the X axis is the number of seconds a given proof took to complete, whereas the Y axis is the percentage of all of the proofs that took less than that X amount of time. By plotting this on a semilog scale in X, you can understand some of the realities of formal verification. For example,

82% of all of the proofs I’ve done have taken less than one minute
87% of all of the proofs I’ve done have taken less than two minutes
93% of all of the proofs I’ve done have taken less than five minutes
95% of all of the proofs I’ve done have taken less than ten minutes

Every now and again, I’ll post about how long a given proof takes. For example, I’ve had proofs require a couple of hours to return. A classic example would be some of the proofs associated with verifying my open source generated FFT cores. Such proofs are the exception rather than the norm, however, and typically when I write about such extreme times its because I wasn’t expecting the proof to take that long to accomplish.

The reality is that I don’t normally notice how long a proof takes. Why not? Because formal verification, in my experience, has typically been faster than simulation. It’s typically faster than running a design through synthesis or place-and-route. This follows from the fact that 95% of all of these proofs were accomplished in less than 10 minutes, whereas it often takes longer than 10 minutes with Vivado to synthesize a design.

How do I keep my proofs that short?

This is a really good question, and there’s typically several parts to the answer.

In general, the amount of time a proof requires is a function of the number of items that need to be checked, and the number of steps they need to be checked in. Of these two, I usually have the most control over the number of steps required by the proof. SymbiYosys calls this the “depth” of the proof.

How shall this depth be set?

For many simple peripheral cores, the depth can be set initially to however long it takes to perform the operation the core is required to perform.

This can often be determined by running a cover() check, and seeing how long it takes the core to complete an operation and to return to idle.

This doesn’t work for all cores, however, but it is a fairly good start. It does apply nicely to most SPI cores, as well as those that are similar such as my MDIO controller, since they all have fixed transaction lengths. It can also apply to CPUs, where the depth is determined by the time it takes for a single instruction to go from when it is issued all the way to when it is retired.
For most of my proofs, I start with a depth set to default, 20 steps. If I struggle inexplicably at that depth, I may set it to longer as a result of a basic knee-jerk reaction.

The fact is, when you first start out with a formal proof, the solver can typically find assertion failures very quickly. It’s only as you slowly remove these initial failures that the proof starts to take the solver more and more time to return an answer.
If the solver takes too long at a depth of 20, I’ll often shorten the depth.

This was the case with my AXI crossbar. AXI is such a complicated protocol, I couldn’t let the depth get too long at all. In the end, I fixed this depth to four time-steps. It was the shortest depth I could find where all of the various constraints could be evaluated properly in the time interval.

One of the nice features of Yosys’ SMT solver is that it reports back periodic status messages showing how long each step has taken. This helps you know where the “limit” is. For example, if the first five steps take less than 6 seconds each, but the six step has taken over an hour and it hasn’t yet completed, you may need to drop the depth to five and just work with it there.
The trick to setting the depth is induction.

If the inductive step ever passes, even if I don’t have all of the properties I want in place yet, I’ll set the depth to whatever it took to pass induction. This keeps the proof as short as it will ever be.

For example, the ZipCPU can be formally verified in between 10 and 14 steps depending upon the configuration. Given that each step is longer than the step before hand, it makes sense to keep the solver from doing too much. Those configurations that can be solved in 10 steps I set to be solved in 10 steps. Those that cannot, get set to however many steps they need. While this won’t speed up the inductive step at all, it often shortens the associated basecase.
How do you know your depth is too shallow?

I’ve had several proofs that have required depths of much longer than ten or twenty steps. Examples include my serial port receiver (an asynchronous proof) at 110 clocks, my hyperram controller at 40 clocks, and several of the slower configurations of my universal flash controller ranging from 26 steps all the way up to 610. Cover proofs tend to be worse than assertion based proofs, with my serial port receiver requiring 720 steps, and the MDIO controller for my ethernet implementations requiring 258 steps.

The easy way to know that a proof isn’t too shallow is to work with induction until it passes as we just discussed above. In the case of cover, covering intermediate states will help to reveal just how long the trace needs to be.

Knowing if an induction proof is too shallow requires understanding your core, and the trace produced during induction.

As I teach in my formal methods course, there are three kinds of assertion failures during induction: 1) those that fail at the last time step, 2) those that fail the time step before that, and 3) those whose failure can be tracked to earlier in the trace. Typically, in the third case, an assertion is sufficient to bring the design back in line. If the data necessary to make the assertion isn’t part of the trace, such as if it’s dependent upon something that happened earlier, then you either need to add a register to capture the dependency or you need to increase the depth of the trace.

The reason that my serial port receive proof is so long is that I had a criteria that the clock in the serial port transmitter would never be off by more than half a baud interval at the end of the transmission. Measuring how far that would be at every time step required a multiplication function–something that doesn’t work well with formal methods. As a result, I was forced to only checking this value at the end of every baud interval, and using power-of-two properties. This fixed the induction length to at least one baud interval in length.
Some problems are just too hard

Two classic examples are multiplies and encryption. Of the two, formally verifying designs with multipliers within them is an area of active research. I wouldn’t be surprised to see some breakthroughs in the near future. Formally verifying designs with encryption within them should be and should remain a hard problem, otherwise the encryption isn’t worth its salt.

I like to get around this problem by replacing the internal multiplier or encryption result with a solver chosen value. This can work for DSP problems, making it possible to still apply formal methods to DSP algorithms although the result is often not quite as satisfying.

The Beginner Mistake

The big mistake I’ve seen beginners make is to take a large and complex core, often one with several component files having no formal properties, and then try to formally verify that a single property holds for all time.

This is a recipe for both frustration and failure.

A classic example would be a user who finds a CPU core on opencores, knows nothing about it, but still wants to know if an assertion about it will pass.

Instead, start your formal verification work at the bottom level of a design with what I often call “leaf modules”–modules that have no submodules beneath them. Formal verification, and particularly verification using induction, is not a black box exercise. Passing an induction test requires an intimate knowledge of the design in question, and several assertions within the design. Building those assertions from the bottom up makes it easier to get a property to pass later at the top level.

I should mention that there are several solvers that do not require this intimate internal knowledge, such as the abc pdr solver or either of the aiger solvers aiger avy or aiger suprove, and so I’ve seen beginners attempt to use these solvers for this purpose as well. Sadly, these solvers are not well suited for such large designs, and they tend not to provide any progress feedback along the way. The result tends to be user complaints that the solver hangs or crashes, when in reality the problem was that the user was expecting too much from the tool.

This is also one of those reasons why formal verification works so well at the design stage, rather than as a separate verification stage done by a new team of engineers. It is the designer who knows how to constrain the values within his own design–not the verification engineer.

Conclusion

Despite its reputation for computational complexity, hardware formal verification tends to be very fast in practice today. It’s often faster than both simulation and synthesis, allowing a designer to iterate on his design faster than he would with either of these other approaches.

If you’ve never tried formal verification, then let me invite you to work through my beginning verilog tutorial. Once you get past the second lesson, every design will involve formally verifying that it works before ever trying to implement the design on actual hardware. Indeed, the background you will need for more complicated projects is to be gained by working on simpler projects–as it is in many other fields.