Answer to Quiz #17
 |
Let’s illustrate this with a fun example: a counter. We’ll have this counter
down from some MAX_VALUE down to zero.
always @(posedge i_clk)
if (i_reset)
counter <= 0;
else if (counter > 0)
counter <= counter -1;
else if (i_start)
counter <= MAX_VALUE;We’ll also use a flag to identify every time this counter is zero.
always @(posedge i_clk)
if (i_reset)
zero_counter <= 1;
else if (counter > 0)
begin
if (counter == 1)
zero_counter <= 1;
end else if (i_start)
zero_counter <= 0;Now, let’s make sure zero_counter is always raised when the counter finally
returns to zero.
always @(posedge i_clk)
if (f_past_valid && !$past(i_reset) && $past(counter == 1))
assert($rose(zero_counter));This assertion will fail induction.
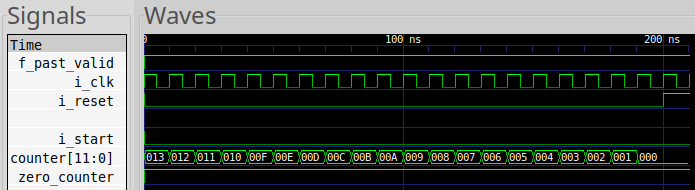
Why? Because, if MAX_VALUE is longer than your induction length, then the
induction engine will start from a time when counter > 0 and zero_counter=1.
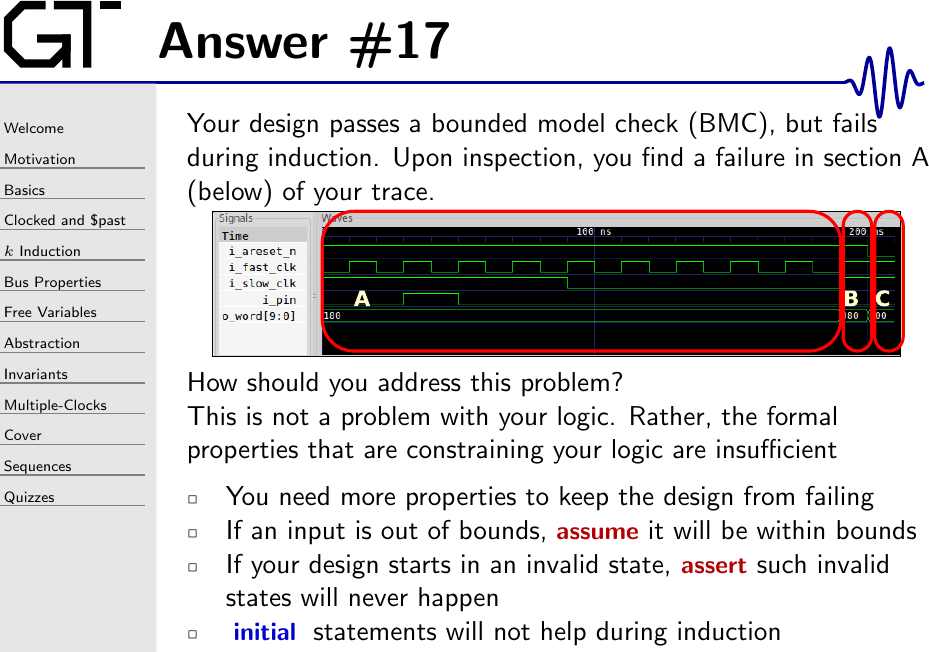
You’d be able to see this in section A of the trace below.
 |
This would be a fault, but it’s not the one that our property above is
catching. Instead, you’d catch the fault above and then examine the formal
generated trace. You’d then follow the failed assertion up stream and scratch
your head wondering why zero_counter = 1 at a time when counter > 0.
The solution to this problem is to make it clear to the formal solver how
counter and zero_counter are supposed to be related.
always @(*)
assert(zero_counter == (counter == 0));Once you do this, the problem will go away.
Note that this problem is unique to how certain solvers handle induction.
