Answer to Quiz #11
 |
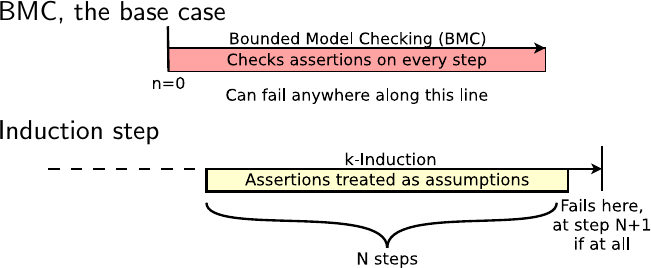
Here’s the problem: when using
induction,
the induction
engine is free to start the design in any state it wants subject to the only
constraint that the first N cycles don’t violate any assumptions
or assertions. What that means is that your design can start in an
unreachable state.
 |
We discussed this on the blog in the post titled, “An Exercise in Formal Induction”. Indeed, that post deals with this same problem just revealed in a different context.
The trick with using
induction
is to make certain that the design can never spend N cycles within any
unreachable set of states. This is the purpose of answers 2 and 3 above.
Of the two, answer 3 is probably my favorite. If you assert that all the bits in the two shift registers will be consistent, then you can verify the design within a cycle or two. Doing this, however, requires that you 1) have access to all of the signals within the design, 2) either recognize this problem when creating it or 3) reverse engineer the design you are verifying enough to realize what’s going on.
This isn’t always possible, in which case answer 2 comes into play.
Answer 2 forces the i_ce signal to be high often enough that the design
can be verified in about 30 steps. You could also force i_ce to be true
every third step,
always @(posedge i_clk)
if (!$past(i_ce) && !$past(i_ce,2))
assume(i_ce);While this works, it will force the proof to take closer to 45 steps.
If you haven’t tried this exercise, I would encourage you to do so. Force
the proof length to be short enough that the
induction
engine fails, and then examine the traces produced by the
induction
engine to see what’s happening. In
particular, look at the values for i_ce chosen by the solver. As the length
gets longer and longer, you’ll see these values tend to stretch like a spring.
It’s a fun exercise, so I’d encourage it.
The first answer above, that of using a different engine, might also work for you. This is a great option to use—when you can. The problem is that some of these “miracle” engines choke on large designs: you’ll run the solver on your design for hours on end, get no information about why its taking so long, and then never know what’s holding it up. When you eventually kill the solver, you’ll never know if it would’ve been another 5 seconds until it would’ve found the solution or another day. The SMT solvers, on the other hand, can often press through to a solution–even if they do struggle with the induction problems such as the one listed above.
A fourth option, not listed in the slide above, is to use
Yosys optimizations so that sa[14] and
sb[1] are kept in the same FF. At that point, the proof becomes trivial
since Yosys treats the two values as
synonyms for each other.
