Answer to Quiz #4
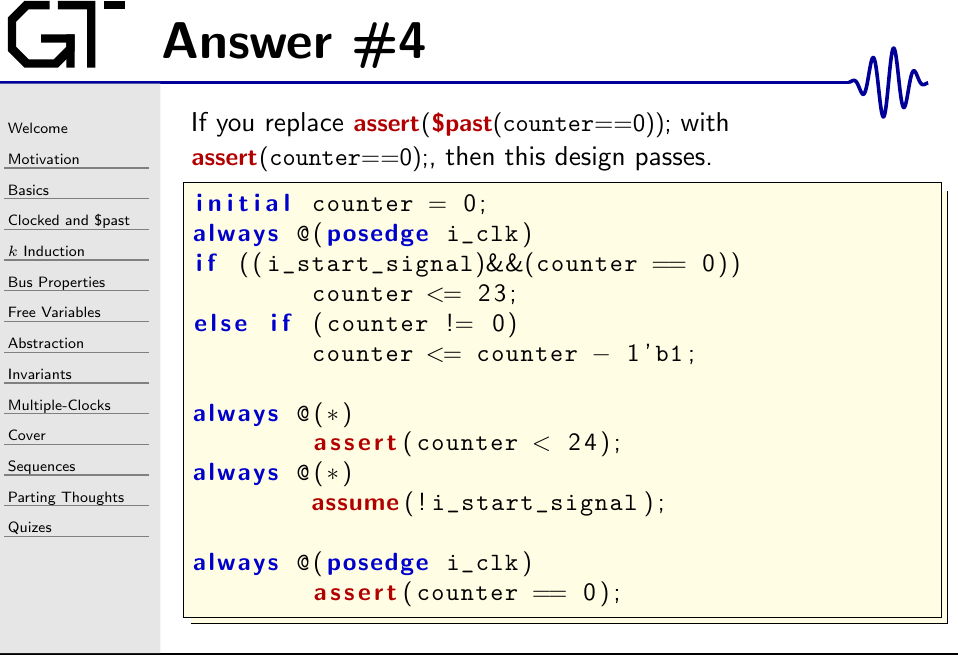 |
As noted above, the design fails because of the $past(counter == 0)
assertion.
The problem here is the reality of how $past(X) is implemented.
Internal to the formal solver, $past(counter == 0) would be replaced
with a past_counter_zero variable (which would actually have a
less than human comprehensible name), defined something like:
reg past_counter_zero;
always @(posedge i_clk)
past_counter_zero <= (counter == 0);As you can see from this example, there’s no initial value to this register.
This is one of the reasons why I place an f_past_valid register into my
designs. Had we done so, the assertion would’ve passed.
reg f_past_valid;
initial f_past_valid = 0;
always @(posedge i_clk)
f_past_valid <= 1;
always @(posedge i_clk)
if (f_past_valid)
assert($past(counter == 0));Alternatively, if you had the Symbiotic EDA Suite, you might have just validly written,
assert property (@(posedge i_clk)
1 |=> $past(counter == 0));While both of these would’ve passed, they would’ve taken an extra step in the solver to first generate the past value and then to check it. Wouldn’t it make more sense to just,
always @(posedge i_clk)
asssert(counter == 0);This is one of my (many) reasons for advising against constraining the past.
Your assertions should constrain registers in their current state,
(assert(counter == ...))
referencing the past if necessary,
rather than constraining any past values (assert($past(counter) ==...)).
We could even go one step further, and create an assertion with no dependency
on $past() at all, evaluated at all time steps.
always @(*)
assert(counter == 0);This is often a better assertion. It takes one less step to trigger, and so
it triggers at the last step in the trace–rather than the penultimate step.
Where @(*) assertions really shine, however, is in asynchronous contexts,
where they are evaluated on every formal time-step rather than just at the
clock edges.
Of course—the assumption that i_start_signal will always be zero rather
violates the spirit of this design. Is there a way to prove that the
counter will remain zero if i_start_signal is never raised?
Were I to try to maintain the assumption, I might choose to use an
(* anyconst *) signal.
(* anyconst *) reg check_start_signal;
always @(*)
if (check_start_signal)
begin
assume(!i_start_signal);
assert(counter == 0);
endThat’s how I’d set a check up to check for something requiring an assumption to set up the right circumstance.
In this case, even that’s not really what you want. Instead, it would make more sense here to just check the transition.
always @(posedge i_clk)
if (f_past_valid && $past((counter == 0) && !i_start_signal))
assert(counter == 0);Or, using concurrent assertions,
assert property (@(posedge i_clk)
(!i_start_signal) && (counter == 0)
|=> (counter == 0));This does a better job capturing the spirit of the logic, as well as the spirit of the (broken, but now fixed) assertion.
