Building a video controller: it's just a pair of counters
When I first started working with FPGAs on my own, the board I started with was a Basys3 board. As a new student of FPGA design, and particularly one on a budget, I wanted to create a series of designs that would eventually use all of the hardware ports of that board. You know, get the most for your money? Hence the question, how best should I use the VGA port?
My original thought was to use the VGA
port was to create a
screen buffer, and then
to display that buffer. The only problem was that a
screen buffer
big enough to hold a 640*480 screen requires 307kB of buffer space, and the
Basys3
board didn’t have any external RAM memory, and the Artix-735T
sold on the
Basys3
board didn’t have enough block RAM for such a buffer.
How to solve this?
Eventually, I settled on an approach that used a 25MHz pixel clock and flash memory. Of course, the flash memory wasn’t fast enough to drive the 25MHz pixel clock, so I instead run-length encoded the image data and dropped the bits per pixel down to a four bit value that could then used in a color table lookup to get full 12’bit color which was all that the Basys3 board supported.
If you’ve worked with FPGAs for a while, you’ll quickly recognize that every step in this increasingly complex processing chain is an opportunity for things to break. The flash controller needs to work perfectly, the memory reader that feeds the FIFO needs to work perfectly, and then the decoder needs to work perfectly. One missed pixel and the entire decompression chain will produce a garbage output for the rest of the frame.
Oh, and did I mention the ZipCPU was also trying to use the memory on this little board at the same time?
The traditional way I’ve seen others decode things like this in the past is to use some form of scope applied to the horizontal and vertical sync’s of the video image. This would confirm that the video sync signals were being properly sent to the screen. The problem with this approach is that you’ll never have enough fingers to get a trace from all of the video wires and, worse, even if you did you’d struggle to decipher the traces without any other context.
As I’m sure you can imagine, this approach didn’t work for me.
The reason it didn’t work is that the image might decode nicely for half the screen, and then somehow get off cut and then it would degrade into decompressed chaos. Well, that and I didn’t own an oscilloscope until much later.
Instead, I chose a different approach: Verilator based video simulation. Using a video simulator, I could slow things down and even stop the simulation anytime something “wrong” showed up on the screen and go back and debug whatever the problem was.
Today, let’s talk about how the simulator works, and then walk through a demonstration design that will draw some color bars onto a simulated video screen.
The VGA Simulator
If you’ve never tried this VGA simulator before, you can find it on github, separated into its own repository. The simulator depends upon the gtkmm-3.0 library, and so on the libgtkmm-3.0-dev Ubuntu package. (It might even run on Windows under Cygwin, I just haven’t tried it.) If you have both Verilator and this library installed, you should be able to run the demo by typing:
% git clone https://github.com/ZipCPU/vgasim
% cd vgasim
% make
% cd bench/cpp
% ./main_tb -g 640x480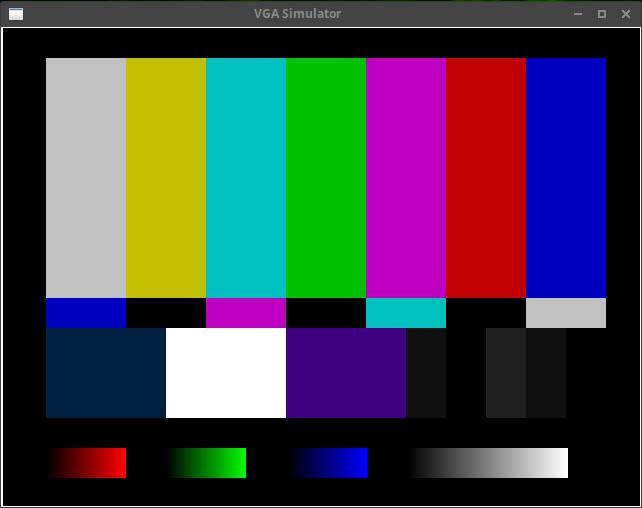 |
If all goes well, you should see the image at the right within a window on your screen. You can kill the program by either typing control-C in your bash window, or by clicking on the close box of the window it creates.
Let’s examine this image for a moment.
First, the image in Figure 1 very carefully has a white box around the border of the image. This box denotes the first and last pixel of every line, as well as the first and last line of every frame. It’s an important test for this reason first: it shows if you’ve lost any pixels due to timing, as these will otherwise fall off the screen.
Second, the image explores the color space of your video output. Notice the many shades of red, green, blue, and gray at the bottom of the image.
Third, but perhaps not so obvious, no image would be possible without creating a proper VGA signal. This means that behind the scenes, there needed to be horizontal and vertical sync channels as well as three serial streams of data that all had to line up properly together.
Finally, it just looks like an old fashioned TV test image.
 |
If this isn’t enough to get your interest, then let me offer some other
capabilities found within the repository. First, if you have the screen space
to run the simulator with a sub-window of
1280x1024 (main_tb with no arguments), you can see the results of a more
typical frame buffer
implementation, shown (shrunken) in Fig. 2 on the left.
The third demonstration within the VGA
simulation repository is that of a
VGA input
simulator, such as might come from a camera. This simulation is built as the
simcheck executable within the same bench/cpp directory. To run it,
simply type:
% simcheckAs before, you can kill this simulation by either Ctrl-C or clicking the close button on the window.
What does this input/camera simulator do? It creates a VGA inputs to a design. It creates these inputs from a input image obtained from the top left corner of your screen. You can then process that input within your Verilated Verilog design to your hearts content. Alternatively, you can send the inputs from the VGA input simulator directly into the regular VGA simulator to see it on the screen.
What’s really fun about this camera simulator is when you overlap the output window with the camera “input” area, you can get some really neat effects, such as are shown in Fig 3. below.
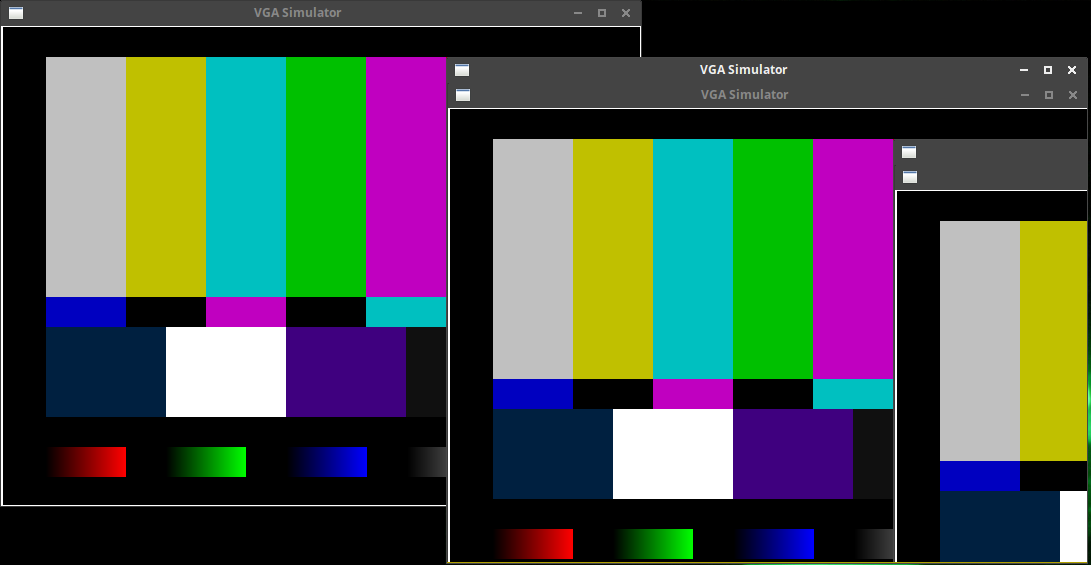 |
In this image, the window at the top left is the same VGA simulation output display program shown in Fig. 1. What’s different is the second window just to the right and below it. This is the VGA simulation output that just reflects the source information to the simulated output. The third “window” showing further to the right is the recursive effect I was just mentioning. In reality, there’s no “window” there, but just a recreation of the top left 640x480 pixels of the image.
Shall we dig into the simulator a bit and see how to use it?
The Wiring
The VGA simulator is based around the VGA signaling standard. Yes, I know this is an older standard, but it’s also an easy one to learn from. I do have an HDMI simulator lying around that is very likely to eventually join this repository …
But back to VGA.
The VGA standard consists of five signals.
-
o_vga_vsync, the Vertical sync (pronounced “sink”), 1’bit -
o_vga_hsync, the Horizontal sync (pronounced “sink”), 1’bit -
o_vga_red, Red pixel component, up to 8’bits -
o_vga_grn, Green, etc. -
o_vga_blu, Blue, etc.
The simulator accepts any color depth up to 8-bits per pixel. Anything over 8-bits, and it just pays attention to the top 8-bits.
To use the simulator with your design, you need to build a Verilator test-bench wrapper around the design, tell the test bench what resolution you want the window to have, and then call the video subsystem to pay attention to video events while running your design.
// ...
#include <verilated.h>
#include "Vyourdesign.h"
//
#include "testb.h"
#include "vgasim.h"
// ....
int main(int argc, char **argv) {
Gtk::Main main_instance(argc, argv);
Verilated::commandArgs(argc, argv);
bool test_data = false, verbose_flag = false;;
char *ptr = NULL;
int hres = 1280, vres = 1024;
// ...
tb = new TESTBENCH(hres, vres);
tb->test_input(test_data);
tb->reset();
// tb->opentrace("vga.vcd");
Gtk::Main::run(tb->m_vga);
}Then, within the tick() method of this test
bench,
the simulator is called with the output values from your
Verilator core:
void tick(void) {
m_vga((m_core->o_vga_vsync)?1:0, (m_core->o_vga_hsync)?1:0,
m_core->o_vga_red,
m_core->o_vga_grn,
m_core->o_vga_blu);
TESTB<Vyourdesign>::tick();
}That’s how you hook up your design, but what do those various signals carry?
Let’s consider the o_vga_hsync, or horizontal sync, signal first. In an old
fashioned cathode ray-tube monitor, this VGA signal would tell the underlying
ray subsystem when to quickly move back from the right side to the left side
of the screen.
The signal itself is an active low signal, as shown in Fig. 4 below.
 |
The signal should be high at all times except during the Horizontal Synch pulse, where it is low. Between the sync pulse and the data is the “back porch”, and then again on the other side between the data and the sync is a “front porch”. While these may seem to be just idle clock periods, they are actually carefully timed and required by the video subsystem.
The simulator needs to be told what these time periods are. This is done within the videomode.h file, a portion of which is shown below:
VIDEOMODE(const int h, const int v) {
m_err = false;
if ((h==640)&&(v==480)) {
// 640 664 736 760 480 482 488 525
setline(m_h, "640 656 752 800");
setline(m_v, "480 490 492 521");
} else if ((h==720)&&(v == 480)) {
setline(m_h, "720 760 816 856");
setline(m_v, "480 482 488 525");
} else if ((h==768)&&(v == 483)) {
setline(m_h, "768 808 864 912");
setline(m_v, "483 485 491 525");
// ...
} else m_err = true;
}Here you’ll see that, internal to the simple WIDTHxHEIGHT video mode call, horizontal and vertical video mode lines are set according to the old XFree86 modeline “standard”, as illustrated in Fig. 5 below.
 |
The first number is the number of valid pixels in the line, it counts from the left to the width of the line. Don’t be confused by Fig. 5 trying to show the relationship of the sync line to the valid pixel data, the sync line is high during this period. The second number includes the additional width of the front porch, but remains measured from the left edge. The third number adds the width of the sync, while the fourth number is the total number of pixel clock intervals before the pattern repeats.
 |
The vertical sync mode is similar. It also consists of the same intervals: valid pixel (line) data, back porch, sync, and front porch. The big difference is that instead of counting pixel clocks, the vertical mode line counts horizontal lines. Further, these horizontal lines are counted from the beginning of the horizontal sync interval. This yields to the apparent discontinuity shown in Fig 6. on the right. This discontinuity only exists, however, because we’ve chosen to place the image at the top-left of our coordinate system. Had we started at the beginning of the horizontal and video sync joint intervals, there would be no apparent discontinuity.
Fig. 6 should also give you a good idea of how to start building a basic video system: with horizontal and vertical position counters. Let’s try that, and see how far we can get!
The Concept
The demonstration design within this VGA simulation repository consists of a couple basic components, as shown in Fig. 7.
 |
Let’s quickly walk through the pieces of this design, and then spend some time digging into the llvga.v and vgatestsrc.v components.
The overall design consists of both a memory device and a video frame controller. We’ve discussed this memory device before, so we need not discuss it again here. The memory is controlled by a wishbone master and video controller, wbvgaframe.v. Within this controller, there’s a component to read frame-data from the memory using the memory/bus clock, and then to cross clocks via an asynchronous FIFO to the pixel clock domain. Once in the pixel clock domain, pixels are then fed to the low level VGA signal generator. Internal to this lower level VGA signal generator is the test-source generator that produced the image shown in Fig 1 above.
While we’ve discussed many of these components on the blog before, such as the memory, the wishbone bus, and the asynchronous FIFO, there are several components of this design that we haven’t discussed before. Today, let’s examine the lower-level VGA generator and the test-bar signal generator.
 |
The lower-level VGA signal generator is designed to interact with the pixel generation subsystem (wbvgaframe.v), and to produce the necessary video signal outputs in order to generate the images above. Here you can see in Fig. 8 the ports necessary to do this. We’ve already discussed the ports on the right above, albeit under slightly different names. The new ports are those on the left. While the reset port might be obvious, the others might need a bit more explaining.
-
i_pixclkI normally name all my incoming clock signalsi_clk. This has become habit forming to me. Not so with this module. In the case of many video signals, the pixel clock runs at a different rate from the main system clock. Hence, I’ve reservedi_clkfor other parts of my design. This component acts upon the pixel clock,i_pixclk, alone. -
i_testis a flag that I use to tell the controller to produce the test bars output I demonstrated in Fig 1. above. Ifi_testis not set, the controller will source its pixels externally fromi_rgb_pix, otherwise it will source the pixels from the internal VGA test source generator. -
o_rdis the first of three pipeline control signals used to help the pixel generator, either imgfifo.v or vgatestsrc.v in this design, know when to generate to pixels. It functions very much like the!stallsignal in the “simple handshake” pipeline strategy we presented earlier.Only, this signal is a little trickier than a negated stall signal. The pixel generator is expected to set up a pipeline filled with pixels and then wait for this signal to go high. Once this signal goes high, pixel data will flow. The pixel generator needs to be careful to never let the pixel feed buffer empty, or catestrophic things may happen. (i.e., the display won’t show the image we want)
-
The
o_newlinesignal is used to indicate that the last pixel in the row has been consumed, and the pixel generator is free to flush any line buffers and start over if it wishes to.In this demonstration design, the
o_newlinesignal is only used by the test image generator. We’ll look at that further down. -
The last pipeline indication signal is the
o_newframesignal. This signal is very much like theo_newlinesignal, save that it indicates the end of the frame as well as the end of the line. This signal is to be true on the last pixel of the frame, and then only. The demonstration frame buffer uses this signal to flush its buffers and start reading from the top of the image.In the old arcade days, this signal might create a “vertical refresh” interrupt to signal the start of the vertical refresh period. This was a time when screen memory was not being read and so software could quickly draw to the screen in a way that wouldn’t flicker. Such “Flickering” can be caused by a software update to the frame buffer, typically consisting of both an erase operation and a redraw, taking place during the active portion of the image, so that the user sees alternately the “erased” portion and the newly drawn portion. This can be fixed by double buffering, so that the partially drawn image never ends up in the live frame buffer. Doing so requires knowing when to swap buffers, and the
o_newframesignal will facilitate that request.
This lower-level VGA generator may be the simplest component of the entire display system: It’s just a pair of counters! So, let’s see how much this low-level VGA controller can accomplish from two separate counters.
First, let’s accept as inputs all of the various components of the two video mode lines. These are simply passed through from the top-level Verilator simulation,
void init(void) {
m_core->i_hm_width = m_vga.width();
m_core->i_hm_porch = m_vga.hporch();
m_core->i_hm_synch = m_vga.hsync();
m_core->i_hm_raw = m_vga.raw_width();
//
m_core->i_vm_height = m_vga.height();
m_core->i_vm_porch = m_vga.vporch();
m_core->i_vm_synch = m_vga.vsync();
m_core->i_vm_raw = m_vga.raw_height();
//
// ...
}as inputs to the top level design, and then down on to this lower level controller.
input wire [HW-1:0] i_hm_width, i_hm_porch,
i_hm_synch, i_hm_raw;
input wire [VW-1:0] i_vm_height, i_vm_porch,
i_vm_synch, i_vm_raw;While we are going to allow these values to be practically anything within this lower level controller, they do require a particular order between them. Specifically, they need to be strictly increasing,
i_hm_width < i_hm_porch < i_hm_synch < i_hm_raw, and
i_vm_height < i_vm_porch < i_vm_synch < i_vm_rawand there is a minimum width and height. When we get to formal verification, we can use the following assumption to capture this required ordering.
always @(*)
begin
assume(12'h10 < i_hm_width);
assume(i_hm_width < i_hm_porch);
assume(i_hm_porch < i_hm_synch);
assume(i_hm_synch < i_hm_raw);
assume(12'h10 < i_vm_height);
assume(i_vm_height < i_vm_porch);
assume(i_vm_porch < i_vm_synch);
assume(i_vm_synch < i_vm_raw);
endThis will force the width to be at least ten pixels wide, likewise for vertical. The other three numbers of each mode line are also required to be in strict increasing order.
This allows us to create a simple counter to keep track of our horizontal position.
initial hpos = 0;
always @(posedge i_pixclk)
if (i_reset)
hpos <= 0;
else if (hpos < i_hm_raw-1'b1)
hpos <= hpos + 1'b1;
else
hpos <= 0;A similar counter can be used to keep track of our vertical position.
Well, it’s not quite that simple. We also need to generate the horizontal
sync signal as well as our pipeline control signals. The obvious signal
we could set within this same loop is the o_newline signal. As discussed
above, this signal is true for one-clock only at the very last pixel of any
line.
The next item to create in this block is a little less obvious. This is the
hrd signal. We’ll use this in a bit to indicate a valid pixel, but we’ll
need to couple it with a simple vrd signal from the vertical direction first.
Put together, this expands our logic a bit more, but it’s still fundamentally a counter–we just set two other signals within this block as well.
initial hpos = 0;
initial o_newline = 0;
initial o_hsync = 1;
initial hrd = 1;
always @(posedge i_pixclk)
if (i_reset)
begin
hpos <= 0;
o_newline <= 1'b0;
o_hsync <= 1'b1;
hrd <= 1; // First pixel is always valid
end else
begin
hrd <= (hpos < i_hm_width-2)
||(hpos >= i_hm_raw-2);
if (hpos < i_hm_raw-1'b1)
hpos <= hpos + 1'b1;
else
hpos <= 0;
o_newline <= (hpos == i_hm_width-2);
o_hsync <= (hpos < i_hm_porch-1'b1)||(hpos >= i_hm_synch-1'b1);
endCan you still see the basic hpos counter within there?
Fig. 9 below shows a trace of this simple logic, focused at the end of the line.
For this trace, the line width was set to 640 pixels, hence o_newline
is true on pixel 639, and o_rd drops on the first non-pixel: 640.
 |
In a similar fashion, Fig. 10 below shows the same trace, but zoomed out far enough so that you can see a full between-line interval.
 |
During this interval,
you may notice that our valid pixel signal, o_rd, goes low before the
horizontal sync becomes active (low), and stays low for some period after
the sync becomes inactive again but before the valid pixels start up again.
The vertical counter is similar. The biggest difference is that the vertical counter changes at the end of the horizontal front porch, just as the horizontal sync signal becomes active.
initial vpos = 0;
initial o_vsync = 1'b1;
always @(posedge i_pixclk)
if (i_reset)
begin
vpos <= 0;
o_vsync <= 1'b1;
end else if (hpos == i_hm_porch-1'b1)
begin
if (vpos < i_vm_raw-1'b1)
vpos <= vpos + 1'b1;
else
vpos <= 0;
// Realistically, the new frame begins at the top
// of the next frame. Here, we define it as the end
// last valid row. That gives any software depending
// upon this the entire time of the front and back
// porches, together with the sync pulse width time,
// to prepare to actually draw on this new frame before
// the first pixel clock is valid.
o_vsync <= (vpos < i_vm_porch-1'b1)||(vpos>=i_vm_synch-1'b1);
endPerhaps you noticed that we didn’t set vrd above. Since this signal is
so simple, it can quietly fit into its own block.
initial vrd = 1'b1;
always @(posedge i_pixclk)
vrd <= (vpos < i_vm_height)&&(!i_reset);Now, vrd && hrd will always be true one clock before a valid pixel, as marked
by o_rd. We’ll call this pre-signal w_rd, to indicate that we are using
combinatorial logic (i.e. a wire) for this purpose.
wire w_rd;
assign w_rd = (hrd)&&(vrd)&&(!first_frame);We’ll except the very first frame from this calculation, just to make
certain we’ve given the pixel generator a chance to see the o_newframe
signal before starting. Creating the o_rd signal is then just as simple
as registering this w_rd signal on the next pixel clock.
initial o_rd = 1'b0;
always @(posedge i_pixclk)
if (i_reset)
o_rd <= 1'b0;
else
o_rd <= w_rd;In a fashion similar to our o_newline signal, we’ll create an
o_newframe signal in case our pixel generation logic needs to do some
work to prepare for the next frame.
always @(posedge i_pixclk)
if (i_reset)
o_newframe <= 1'b0;
else if ((hpos == i_hm_width - 2)&&(vpos == i_vm_height-1))
o_newframe <= 1'b1;
else
o_newframe <= 1'b0;You can see these vertical signals together with our horizontal signals in Fig. 11 below.
 |
Notice that o_newframe will only ever be true when o_newline is also
true: both are true on the last pixel of a line. The difference, of course,
is that o_newframe is only true on the last pixel of the last line.
We’ll use this property later to
formally constrain
o_newline.
Likewise, Fig 12 shows the same trace, but only zoomed out so that we can see many lines at once.
 |
Not only can we see many lines at once, but Fig 12 also shows a full vertical
blanking interval, including the front porch, sync, and back porch. You can
recognize these by noticing the relationship of o_vsync to the valid data
marked by o_rd. You can also see where the o_newframe signal is placed
relative to the rest of the intervals: right at the last pixel of the entire
frame.
If you’ve never dealt with video before, it really is just this simple: the synchronization portion is nothing more than a pair of counters! We’ve added additional signals to indicate when line endings and frame endings take place, but that’s really all there is to it.
Since this is just that simple, verifying this component is also very simple. Let’s discuss that next.
Formally Verifying our Counters
When I formally verify a module, I like to think of that module in terms of a “contract”. This “contract” is sort of a black box description of what I expect from the module. In many ways the study of formally verification then becomes the study of how to answer the question, “what sort of contract is appropriate for what I’m building”?
In this case, I’d first want to verify that I am creating the synchronization signals as required.
We can start with the horizontal sync. Before the end of the front porch, the sync should be inactive (high).
always @(posedge i_pixclk)
if ((f_past_valid)&&(!$past(i_reset)))
begin
if (hpos < i_hm_porch)
assert(o_hsync);Then between the end of the front porch and the end of the synchronization section, the horizontal sync should be active (low).
else if (hpos < i_hm_synch)
assert(!o_hsync);Finally, between the end of the synchronization period and the end of the line period, the synchronization should be inactive (high).
else
assert(o_hsync);This exact same logic applies to the vertical synchronization period as well.
// Same thing for vertical
if (vpos < i_vm_porch)
assert(o_vsync);
else if (vpos < i_vm_synch)
assert(!o_vsync);
else
assert(o_vsync);Wow, how simple could that be?
Have we fully constrained our video controller? Not quite.
We still need to make certain that the horizontal position is properly incrementing. (But the code says it is …) For this, let’s just check the past value and contrain the current one based upon that. If the past value is at or beyond the last pixel of the line, then we should be starting on a new line on this clock. Otherwise, we should be incrementing our horizontal pointer.
if ($past(hpos >= i_hm_raw-1'b1))
assert(hpos == 0);
else
assert(hpos == $past(hpos)+1'b1);The vertical counter is similar, save that it only increments at the beginning edge of the horizontal sync period, otherwise it should be the same in all cases.
if (hpos == i_hm_porch)
begin
if ($past(vpos >= i_vm_raw-1'b1))
assert(vpos == 0);
else
assert(vpos == $past(vpos)+1'b1);
end else
assert(vpos == $past(vpos));These two constraints, however, aren’t enough to keep the two counters within their limits. To do that, we need to insist that they are less than the proper raw widths.
assert(hpos < i_hm_raw);
assert(vpos < i_vm_raw);Without these last two assertions, the formal induction step might start our design way out of bounds. Indeed, you should always assert that any state variables are within bounds! That’s the purpose of these last two assertions.
At this point, we’ve created enough assertions to guarantee that a monitor capable of synchronizing to this signal will do so.
Everything else is icing on the cake.
We first have our o_rd value which will signal to the part of the design
that sends us pixels that we just accepted a pixel. This value should be
true during any valid pixel period. We can check this simply with,
if ((hpos < i_hm_width)&&(vpos < i_vm_height)
&&(!first_frame))
assert(o_rd);
else
assert(!o_rd);That leaves two other signals: the newline signal and the new frame signal. The newline signal is true on the last clock period of any line. We can assert that here.
if (hpos == i_hm_width-1'b1)
assert(o_newline);
else
assert(!o_newline);Finally, the o_newframe signal needs to be true at the same time as
o_newline, but only on the last valid line. Otherwise this should be zero.
if ((vpos == i_vm_height-1'b1)&&(o_newline))
assert(o_newframe);
else
assert(!o_newframe);There is one catch in all of this simplicity: our assertions above will fail if the video mode is changed. This I found annoying, since I had written the code above to be self correcting upon any mode changes, yet I struggled to find a way to formally verify this code as self correcting–the solver just kept changing the mode line every chance it could. As a compromise, I only check the above properties if the video frame is stable. To do that, I capture the video mode for the last clock, both horizontal and vertical mode signals,
wire [47:0] f_vmode, f_hmode;
assign f_hmode = { i_hm_width, i_hm_porch, i_hm_synch, i_hm_raw };
assign f_vmode = { i_vm_height, i_vm_porch, i_vm_synch, i_vm_raw };
reg [47:0] f_last_vmode, f_last_hmode;
always @(posedge i_pixclk)
f_last_vmode <= f_vmode;
always @(posedge i_pixclk)
f_last_hmode <= f_hmode;I know these are stable when their values are the same as they were one clock ago.
reg f_stable_mode;
always @(*)
f_stable_mode = (f_last_vmode == f_vmode)&&(f_last_hmode == f_hmode);While I could assume that the mode was always stable, I would like to make this design able to change modes. (The simulator cannot change modes, but this portion of the design can.) For this, I just insist that the modes are identical unless the reset line is high.
always @(*)
if (!i_reset)
assume(f_stable_mode);I can also hear some of you asking, why did I create f_last_hmode and
f_last_vmode? Why not just use the $past() operator? Even better, the
$stable() operator, short hand for X == $past(X), would perfectly describe
our situation. Why not just say instead,
always @(posedge i_clk)
if (!i_reset)
assume(($stable(f_hmode))&&($stable(f_vmode)));The answer is subtle, and reveals a bit about how
SymbiYosys works.
The $past(X) operator, though, requires
a clock. Because of that, it isn’t evaluated until the next clock edge.
(This is why assertion failures for clocked blocks appear at the penultimate
clock edge.)
Where this becomes a problem is when the design fails at the final clock
edge, because the assumption hasn’t taken effect yet. By creating our own
version of $stable() above using f_last_hmode and f_last_vmode, we can
force the mode to be stable on the last cycle–even before the rising edge
would evaluate a $stable(X) operator.
The Test Pattern Generator
 |
Let’s now turn our attention to creating the test pattern. This generator works by calculating a color for each line, and then selecting the right color from among all of the line colors as shown in Fig. 13 on the right.
Well, not quite. Selecting from among 480+ line colors might be more logic than I’d want to use for a simple test pattern generator. Here’s the secret: colors are generated in bands.
What may not be obvious is that the test pattern generator segments the screen into 16x16 sections. Determining what color to generate is mostly just a matter of determining which 16x16 location the current pixel is within. Note that these may not have been the proportions of the original test cards from which these images are (loosely) drawn–but they make the math easy for us and so we use them here.
Calculating the section at issue comes back to the same issue of counters again. The test pattern generator uses one counter for horizontal position, and another for vertical–just like the low-level controller we just examined above.
Let’s start by following the horizontal counter, hpos.
always @(posedge i_pixclk)
if ((i_reset)||(i_newline))
begin
hpos <= 0;
hbar <= 0;
hedge <= { 4'h0, i_width[(HW-1):4] };
end else if (i_rd)
begin
hpos <= hpos + 1'b1;
if (hpos >= hedge)
begin
hbar <= hbar + 1'b1;
hedge <= hedge + { 4'h0, i_width[(HW-1):4] };
end
endOn every new line, this counter resets to zero. Further, on every valid
pixel, the counter moves forward. There’s no checking whether or not the
counter has reached the full width, since that is done via the i_newline
flag.
What may be curious, though, are the two values hbar and hedge.
These variables are associated with dividing the screen into sixteen horizontal
regions. Specifically, the idea is that hbar is the current horizontal pixel
location times 16 and divided by the width.
The problem is division within an FPGA is hard. How can it be avoided?
The first step towards avoiding this is to divide the width by sixteen.
This is easily done by right shifting the screen width by four. We can
then count bins across the screen, where hedge is the end of the next bin.
If you look at Fig. 14 below, you can see how well our division matched the screen.
 |
We can now calculate the colors for the long top bars using a basic case statment. If we are in the first position, output a black, otherwise if we are in the second position, etc.
always @(posedge i_pixclk)
case(hbar[3:0])
4'h0: topbar <= black;
4'h1: topbar <= mid_white;
4'h2: topbar <= mid_white;
4'h3: topbar <= mid_yellow;
4'h4: topbar <= mid_yellow;
4'h5: topbar <= mid_cyan;
4'h6: topbar <= mid_cyan;
4'h7: topbar <= mid_green;
4'h8: topbar <= mid_green;
4'h9: topbar <= mid_magenta;
4'ha: topbar <= mid_magenta;
4'hb: topbar <= mid_red;
4'hc: topbar <= mid_red;
4'hd: topbar <= mid_blue;
4'he: topbar <= mid_blue;
4'hf: topbar <= black;
endcaseThe actual colors are defined as constants earlier in the file.
After the main bars at the top, the alternate colored bars beneath them and lining up with them,
always @(posedge i_pixclk)
case(hbar[3:0])
4'h0: midbar <= black;
4'h1: midbar <= mid_blue;
4'h2: midbar <= mid_blue;
4'h3: midbar <= black;
4'h4: midbar <= black;
4'h5: midbar <= mid_magenta;
4'h6: midbar <= mid_magenta;
4'h7: midbar <= black;
4'h8: midbar <= black;
4'h9: midbar <= mid_cyan;
4'ha: midbar <= mid_cyan;
4'hb: midbar <= black;
4'hc: midbar <= black;
4'hd: midbar <= mid_white;
4'he: midbar <= mid_white;
4'hf: midbar <= black;
endcaseas well as the thicker and wider bars underneath those.
always @(posedge i_pixclk)
case(hbar[3:0])
4'h0: fatbar <= black;
4'h1: fatbar <= purplish_blue;
4'h2: fatbar <= purplish_blue;
4'h3: fatbar <= purplish_blue;
4'h4: fatbar <= white;
4'h5: fatbar <= white;
4'h6: fatbar <= white;
4'h7: fatbar <= purple;
4'h8: fatbar <= purple;
4'h9: fatbar <= purple;
4'ha: fatbar <= darkest_gray;
4'hb: fatbar <= black;
4'hc: fatbar <= dark_gray;
4'hd: fatbar <= darkest_gray;
4'he: fatbar <= black;
4'hf: fatbar <= black;
endcaseThe logic for all three sections is identical at this point.
You may also wish to note that, just like we did with the ALU, we are calculating color bars even when we’ll be outputting the color from a different bar. We’ll do a downselect in a moment to get the right color for each row.
Indeed, when it comes to generating row information, the logic is very similar to the horizontal logic above. We divide the screen by sixteen, and keep track of which sixteenth of the screen we are within at any given time.
reg dline;
always @(posedge i_pixclk)
if ((i_reset)||(i_newframe)||(i_newline))
dline <= 1'b0;
else if (i_rd)
dline <= 1'b1;
always @(posedge i_pixclk)
if ((i_reset)||(i_newframe))
begin
ypos <= 0;
yline <= 0;
yedge <= { 4'h0, i_height[(VW-1):4] };
end else if (i_newline)
begin
ypos <= ypos + { {(VW-1){1'h0}}, dline };
if (ypos >= yedge)
begin
yline <= yline + 1'b1;
yedge <= yedge + { 4'h0, i_height[(VW-1):4] };
end
endThe biggest difference between this logic and the horizontal logic is the
dline item. This is used to keep the i_newline signals following the
i_newframe, but before the first line of the image, from adjusting our
counter. Perhaps you’ll recall from Fig. 12 above that the horizontal sync’s,
and so the o_newline signal, continued even during the vertical blanking
period. dline above helps us avoid counting lines during this period.
You can see how well we did this in Fig. 15 below.
 |
We can then determine the final outgoing pixel by selecting on which sixteenth
of the image vertically we are on. This is captured by the yline value
we just calculated above.
always @(posedge i_pixclk)
case(yline)
4'h0: pattern <= black;
4'h1: pattern <= topbar; // Long top bar
4'h2: pattern <= topbar;
4'h3: pattern <= topbar;
4'h4: pattern <= topbar;
4'h5: pattern <= topbar;
4'h6: pattern <= topbar;
4'h7: pattern <= topbar;
4'h8: pattern <= topbar;
4'h9: pattern <= midbar; // Narrow mid bar
4'ha: pattern <= fatbar; // Thick/wide bars
4'hb: pattern <= fatbar;
4'hc: pattern <= fatbar;
4'hd: pattern <= black;
4'he: pattern <= gradient; // Gradient line
4'hf: pattern <= black;
endcaseAs a final step, we place a white border around our image.
always @(posedge i_pixclk)
if (i_newline)
o_pixel <= white;
else if (i_rd)
begin
if (hpos == i_width-12'd3)
o_pixel <= white;
else if ((ypos == 0)||(ypos == i_height-1))
o_pixel <= white;
else
o_pixel <= pattern;
endThat just about explains everything! The only thing we’ve left out is the gradient sections.
The gradient sections were a bit more challenging. To do them properly, the
image needed to be fully divided, so that a variable hfrac would smoothly
go from zero to overflow as it crossed from one edge of the image to another.
This means that we need to add to hfrac a value equal to one divided by the
image width on every clock tick. Well call this the step size, h_step.
If we knew what h_step was, the logic would be as simple as,
always @(posedge i_pixclk)
if ((i_reset)||(i_newline))
hfrac <= 0;
else if (i_rd)
hfrac <= hfrac + h_step;If hfrac is FRACB bits in width, then h_step needs to be
set to 2^FRACB / width.
Ouch! Divides are hard in digital logic. Do we really have to do a divide?
Can we cheat instead? In this case, we certainly can!
Let’s check at the end of every line how close we came. If we went too far,
then let’s lower h_step, otherwise if hfrac didn’t go far enough, we’ll
increase h_step. It’s a basic control loop solution, and it will take
roughly 2^FRACB/width lines to converge (remember, there are FRACB bits
in our hfrac and h_step. In other words, we’ll converge within about a
hundred lines for 640x480 resolution, or about 64 lines for a 1280x1024
resolution.. This is usually enough to hide the fact that the divide hasn’t
converged until the time that the value is needed.
 |
So, here’s the code for the divide:
always @(posedge i_pixclk)
if ((i_reset)||(i_width != last_width))
// Start over if the width changes
h_step <= 1;
else if ((i_newline)&&(hfrac > 0))
begin
// On the newline, our hfrac value is whatever it ended up
// getting to at the end of the last line
//
if (hfrac < {(FRACB){1'b1}} - { {(FRACB-HW){1'b0}}, i_width })
// If we didn't get far enough to the other side,
// go faster next time.
h_step <= h_step + 1'b1;
else if (hfrac < { {(FRACB-HW){1'b0}}, i_width })
// If we went too far, and so wrapped around
// then don't go as far next time
h_step <= h_step - 1'b1;
endNotice how we just increment or decrement h_step based upon how close
we got to the right answer at the end of the line.
Now that we have this fractional counter that wraps at the line width, we can calculate gradient values for our gradient sections. We’ll set the output (again) depending upon which sixteenth of the horizontal we are in. Only this time, we’ll use the top four bits of this fractional counter to determine the section.
always @(posedge i_pixclk)
case(hfrac[FRACB-1:FRACB-4])
4'h0: gradient <= black;Once you get past this FRACB-4 bit, everything should be incrementing
nicely from the left of the interval to the right.
Our first actual section is red. For this color, we want red pixels ranging
from zero to maximum, and then no blue or grean. (mid_off is an 8'h0).
During this section, we also know that hfrac[FRACB-5:0] will be slowly
counting from zero to overflow as well. If we add a higher order bit,
we can get this gradual counter to gently cross two intervals.
// Red
// First gradient starts with a 1'b0
4'h1: gradient <= { 1'b0, hfrac[(FRACB-5):(FRACB-3-BPC)], {(2){mid_off}} };
// Second repeats, but starting with a 1'b1
4'h2: gradient <= { 1'b1, hfrac[(FRACB-5):(FRACB-3-BPC)], {(2){mid_off}} };(BPC here is the number of “bits-per-pixel”)
A black section, one sixteenth width in length, separates the gradient sections.
4'h3: gradient <= black;Green is roughly the same as red, save only that the first color (red) and the last color (blue) are set to zero. Blue is set similarly. Indeed, if you understand how we did red above, these last two colors are really just the same thing repeated for a different color.
// Green
4'h4: gradient <= { mid_off, 1'b0, hfrac[(FRACB-5):(FRACB-3-BPC)], mid_off };
4'h5: gradient <= { mid_off, 1'b1, hfrac[(FRACB-5):(FRACB-3-BPC)], mid_off };
4'h6: gradient <= black;
// Blue
4'h7: gradient <= { {(2){mid_off}}, 1'b0, hfrac[(FRACB-5):(FRACB-3-BPC)] };
4'h8: gradient <= { {(2){mid_off}}, 1'b1, hfrac[(FRACB-5):(FRACB-3-BPC)] };
4'h9: gradient <= black;The final section is the gray gradient. This one follows the same logic, only we wish to spread it across four regions instead of two. Hence, we’ll force the top two bits to increment across four steps, and use what’s left of the fractional counter to gradually increment.
// Gray
4'ha: gradient <= {(3){ 2'b00, hfrac[(FRACB-5):(FRACB-2-BPC)] }};
4'hb: gradient <= {(3){ 2'b01, hfrac[(FRACB-5):(FRACB-2-BPC)] }};
4'hc: gradient <= {(3){ 2'b10, hfrac[(FRACB-5):(FRACB-2-BPC)] }};
4'hd: gradient <= {(3){ 2'b11, hfrac[(FRACB-5):(FRACB-2-BPC)] }};
4'he: gradient <= black;
//
4'hf: gradient <= black;
endcaseThat’s it for the test
design.
Did you notice the format of the logic?
In general, everything but the y cordinate based variables reset on an
i_newline. Colors were then chosen for each horizontal region, and then a
(nearly final) color choice was made by examining which vertical region
we were in. The last step was to add a white border around the screen,
just to make certain we have our timing right.
Conclusion
Success with video really depends upon your ability to debug your logic. The VGA simulator can make that easier, by allowing you to “see” how your logic actually creates images. Not only that, but because it is a simulation, you can get access to every wire and every flip-flop within it. Want to see how fast the division converges? Want to see what the various video signals look like in practice? Or stop halt a simulation on an error? The VGA simulator can do all that and more.
We also walked through several pieces of a demonstration video design. We discussed the generation of the various video signals, and even walked through how they could be used to create a video test-signal. That said, in many ways we didn’t walk through the critical piece of code required for any frame buffer based design–the code that reads from the frame buffer in memory and sends a valid pixel to our low level controller. This, however, we’ll need to leave for next time.
I know that some have said that VGA is an outdated standard. Everything is moving to HDMI and beyond. Unlike VGA, HDMI is a bit more difficult to generate and work with. There are more steps to it and more protocol missteps that can be made. That said, when I get to the point where I’m ready to post the HDMI simulator, you’ll see that it isn’t all that much more complicated than the VGA simulator we’ve just looked through. Indeed, the same could be said of the MIPI based CSI-2 simulator I have …
For now we see through a glass, darkly; but then face to face: now I know in part; but then shall I know even as also I am known. (1Cor 13:12)
