The last time we discussed how to create a sinewave, we discussed the way to make a very simple sinewave. from a LUT-based table lookup. We limited that sinewave. to an 8-bit table for simplicity, although it could easily be extended to a much larger table.

Today, let’s expand this concept to a sinewave. that uses a quarter wave table made from Block RAM. Such a table uses only a fourth of the block RAM resources required by a full table, although it does require some extra logic to handle making things look like the full table.

Let’s also build this as an example of how to create pipelined HDL logic.

We’ll start by describing the algorithm in general, and then build the algorithm through a series of stages.

The Algorithm

The first step is always stepping back and assessing the problem. If you look at a sinewave, such as Fig 1. below, you can separate the full sinewave period into four sections, one quarter wavelength each.

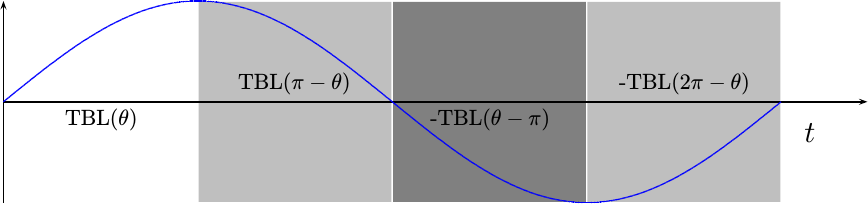Fig 1: Sinewave Symmetry
Sinewave symmetry

We’ll leave the first section alone. This will become our quarter-wave sinewave table. The second section is identical to the first, only in a backwards order. Hence, if we reverse our index, we should be able to recover anything from this quarter wave of the table. The third and fourth sections are identical to the first two, only their results will need to be negated afterwards.

Since we are splitting the full wavelength into four sections, the top two phase bits can be used to determine which of the four sections we are in. If the most significant bit is set, then we’ll want to negate the result. If the next significant bit is set, we’ll want to read backwards out of the table.

This quarter wave table runs into a bit of a problem with phase quantization, though. Consider a phase quantized table with only 16 entries, such as shown in Fig 2.

Fig 2: Sampled Sinewave
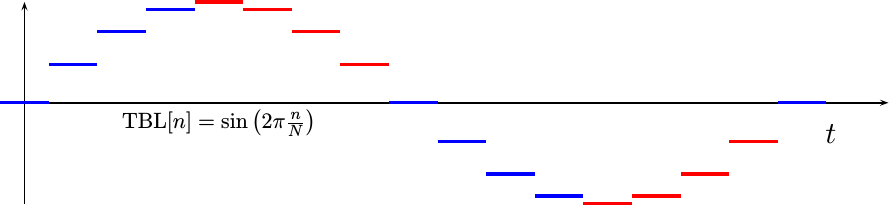Sinewave symmetry broken by sampling

This table has lost the symmetry that was originally present in the sinewave. In particular, table[4]’s value is not present in table[0:3]. If we were to use table[3] to represent the missing table[4] value, we might get a sinewave looking like Fig 3. below.

Fig 3: Symmetry can be broken by quantization
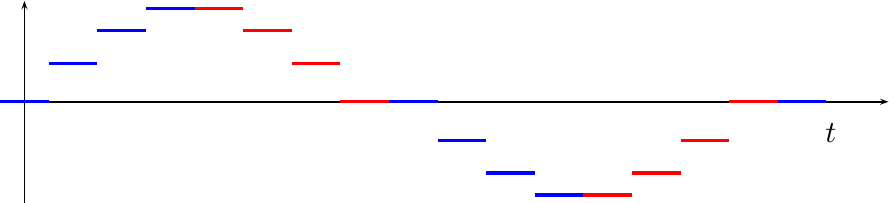Fixing the broken symmetry by shifting a half a sample in phase

Notice how flat the sinewave is every time it crosses zero. It’s not supposed to be this flat. The slope of a sinewave is supposed to be at a maximum when it crosses zero–not flat. This shape distortion will create harmonics that we are not expecting if we don’t fix it.

If we instead advance the sinewave table entries by a half of a sample of phase each, the result will have less harmonic distortion. (i.e., it’ll be closer to the right shape, even if shifted left a touch). The result would then look like Fig 4.

Fig 4: Fixing Symmetry by slipping a half a sample in phase
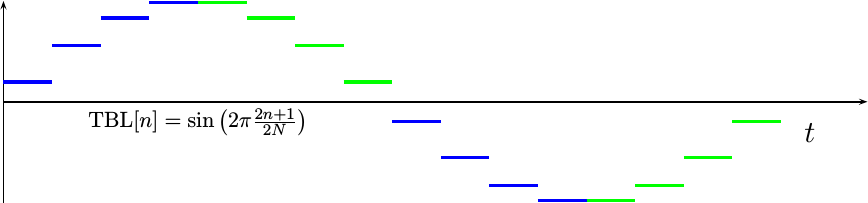Fixing the broken symmetry by shifting a half a sample in phase

The resulting equation for this table is also shown in Fig 4.

The algorithm we want to build will take the first quarter of this sinewave, place it into a table, and then use that same table to generate the other four quarters of the wavelength.

Building the Algorithm

It’s now time to build this algorithm. Although the algorithm itself is quite simple, I’m going to build it in stages and use this as an opportunity to discuss how to build a pipelined algorithm in general. This will allow us to compare several different implementations, and judge between good an bad approaches.

Our first draft for this algorithm uses a giant case statement:

always @(posedge i_clk)
begin
	case({ i_phase[(PW-1):PW-2] })
	2'b00:	o_val <=  tbl[ i_phase[(PW-3):0]];
	2'b01:	o_val <=  tbl[~i_phase[(PW-3):0]];
	2'b10:	o_val <= -tbl[ i_phase[(PW-3):0]];
	2'b11:	o_val <= -tbl[~i_phase[(PW-3):0]];
	endcase
end

In this piece of code, i_phase is the input phase request, tbl is the quarter wave sinewave table, and o_val is the output sinewave. PW is the phase width, or equivalently the number of bits in i_phase.

You may notice that I haven’t used TBLLEN/4-1-i_phase at all when reversing the table entries. Instead, ~i_phase accomplishes the same effect. To know why this is relevant, remember the two steps to negating a two’s complement number: invert all the bits and add one. In this case, we’d subtract one after adding one, so we can just invert the bits. As an example, then, if i_phase counts from 0 to 15, ~i_phase would count from 15 back down to 0.

The problem with this big case statement approach is that most block RAMs are very particular about how they are accessed. Extra logic on the index is not allowed, neither is extra logic on the output. Adding logic in either place can interfere with the synthesis tool and keep it from recognizing your table as a block RAM (or ROM in this case). When dealing with this, I have found the following form to be reliable among the various hardware’s I have worked with.

always @(posedge i_clk)
	if (i_ce)
		tblvalue <= tbl[index];

Perhaps this is simpler than it needs to be, but it does work across vendors’ tool-suites.

This may also be the time to discuss our pipeline strategy. Looking over the various pipeline strategies we posted about earlier, this already looks like the beginning of the “global CE” approach. If we look up the examples of where the “global CE” pipeline strategy makes the most sense, you may recall that DSP logic was one of the common applications of this approach. Since that’s what we are building today, we’ll keep the i_ce line, and add it into the rest of our logic.

Working the simplicity of this block RAM access into our logic, though, will take some work. We’ll need to spend a clock to calculate the index, and another clock after that to deal with the negation.

This brings us to our second approach to our logic.

always @(posedge i_clk)
if (i_ce)
begin
	// First, calculate the table index
	if (i_phase[(PW-2)])
		index <= ~i_phase[(PW-3):0];
	else
		index <=  i_phase[(PW-3):0];

	// Use the index to access Block RAM
	tblvalue <= table[index];

	// Handle the negation afterwards
	if (i_phase[(PW-1)])
		o_val <= -tblvalue;
	else
		o_val <=  tblvalue;
end

This approach still has some hazards to it. Perhaps if we drew a data flow diagram, such as Fig 5 below, these hazards will become be more apparent.

Fig 5: Initial Data Flow Diagram
Initial data flow diagram

Let’s work with this flow diagram for a moment. First, it helps to separate the data flow variables into clock transitions regions. (We’ll show this in Fig 6 below in a moment.) i_phase would be in the first clock. We’ll call this the input clock. index is in the next clock, etc. Once you separate these variables, then you can see the problem with the negation logic. This negation flag needs to come from the high bit of i_phase[(PW-1)], but it has to be available after the table look up. To make this problem more apparent, draw vertical lines through the diagram, dilineating the processing clocks. Data flows should not cross through such lines, without being clocked into a new register–else you’ll have a pipeline bug.

The solution to this problem is to schedule the pipeline logic. Specifically, we’ll create a register to hold i_phase[(PW-1)] while the table index is calculated and the table value is looked up. We can implement this with a two stage shift register, captured by negate[0] and negate[1]:

always @(posedge i_clk)
if (i_ce)
begin
	negate[0] <= i_phase[(PW-1)];
	// ...
	negate[1] <= negate[0];
	if (negate[1])
		// ...
end

A new data flow diagram for this modified algorithm might look like Fig 6.

Fig 6: Scheduled data flow
Data flow diagram, with all logic scheduled

Notice how each variable is now associated with a clock period in the pipeline.

Written out, our logic now looks like:

// Initialize the quarter-wave table
initial	$readmemh("quarterwav.hex", quartertable);

always @(posedge i_clk)
	if (i_ce)
	begin
		// Clock one
		negate[0] <= i_phase[(PW-1)];
		index  <= i_phase[(PW-2)]
				? ~i_phase[(PW-3):0]
				:  i_phase[(PW-3):0];

		// Clock two
		negate[1] <= negate[0];
		tblvalue <= table[index];

		// Output clock
		if (negate[1])
			o_val <= -tblvalue;
		else
			o_val <=  tblvalue;
	end

You can also find a full example of this logic here.

At this point, we are almost done. All that’s left is to create a hex file to be used to crate this table. This can be done from a simple C++ program, where the relevant portion is shown below:

int	tbl_entries = (1 << lgtable),
	maxv = (1 << (ow-1))-1;

for(int k=0; k < tbl_entries/4; k++) {
	double	dv, ph;
	ph = 2.0 * M_PI * (double)k / (double)tbl_entries;
	ph+=       M_PI             / (double)tbl_entries;
	dv = maxv * sin(ph);

	if (0 == (k%8))
		fprintf(hexfp, "%s@%08x ", (k!=0)?"\n":"", k);
	fprintf(hexfp, "%0*x ", (ow+3)/4, (int)(dv) & ((1<<ow)-1));
} fprintf(hexfp, "\n");

Well, not quite. The problem with this approach is that the table generator is closely associtated with the Verilog code itself. In particular, you can’t change the number of table entries, or for that matter the width of the table entries, without also adjusting the Verilog code. For this reason, the C++ generator program creates both the Verilog code and the hex table at the same time.

That’s it! We’ve now made a sinewave generator from just a quarter wave table. We’re still going to need to come back to test this table, to build a test bench and prove that it works, but that’s the basics of the algorithm.

Conclusion

This post is one in a small series of posts discussing how to generate a sinewave. We’ve already discussed a very simple sinewave generator, and we are well on our way to creating and explaining a full blown CORDIC sinewave implementation.

These sinewave generators will then form the basis for testing the digital filters that I intend to discuss and demonstrate as well.

So, while this is the end of this post, in many ways it is only one step forward in building Digital Signal Proccessing algorithms within an FPGA. Stick around, there’s a lot you can do with a sinewave.