Answer to Quiz #14
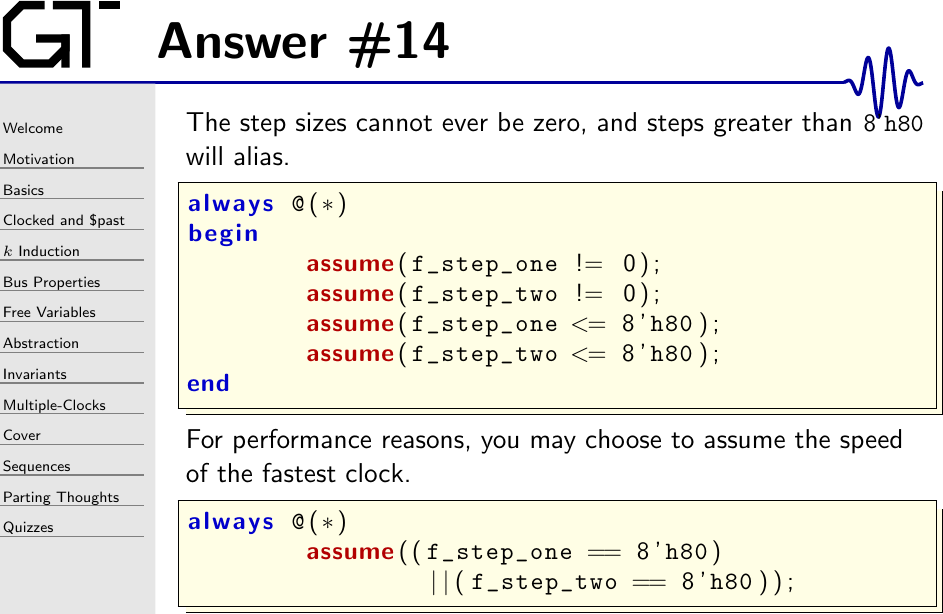 |
Above, you can see my two favorite assumptions.
First, we assume that the step size is never zero. Not all designs require this assumption, but if you want to skip it you might have a challenge passing induction. Why? Well, the induction engine is known for doing such crazy things as keeping the clock idle until the very end of the trace. Then, just before the end of the trace, a single clock edge will take the design from a (not-illegal) state to one that violates an assertion. Worse, it doesn’t matter how long your proof is–adding more steps to the proof doesn’t help in this case. However, if you force the clocks to always step forward, you can keep this situation from happening.
This criteria is closely related to the usage of $past(). If you want to use
$past() with either of the two clocks above, you’ll need to guarantee that
there’s at least two clock ticks within the duration of your proof–one of
which will actually set the $past() value and guarantee its relevance to the
design, and the second of which will test it. (Otherwise, the solver might
start with $past() being anything–an ugly failure mode that you’d never be
able to observe on the trace.) If you also have very slow clocks, this will
also drive the duration of your proof. In the example above, for example,
the proof will need to be a minimum of 258 steps to guarantee a second clock
edge before the final one.
A tedious, but alternative, way of working around this is to make all of your
assertions run combinatorially, always @(*), and to implement $past()
yourself. Indeed, I found this to be the key to getting my asynchronous
FIFO proof down
from a rough hour to less than a second–but I digress. (Note that these
updates were part of a rewrite of the entire
asynchronous FIFO,
and took place after writing my article on verifying an asynchronous
FIFO.)
The other assumption above simply keeps the solver from working too hard. Once the clock step size becomes greater than a half interval, the clock frequency will stop increasing as the step size increases anymore. Indeed, the clock frequency will then go down as the step size increases due to a phenomenon known as aliasing. If we instead assume that the clock frequency stays at a half interval or less, we can keep the solver from examining the alias frequencies. This also has the helpful side-effect of making any resulting traces more comprehensible.
